定理:平面汇交力系的合力对于平面内任一点之矩等于所有各力对于该点之矩的代数和。数学表达式为

M₀(F_R)=M₀(F₁) +M₀(F₂) +…+M₀(F_n)     (2-2)

例2-3如图2-14 所示，一轮盘上C点受到拉力F的作用，试求该力对轮盘0点的矩。

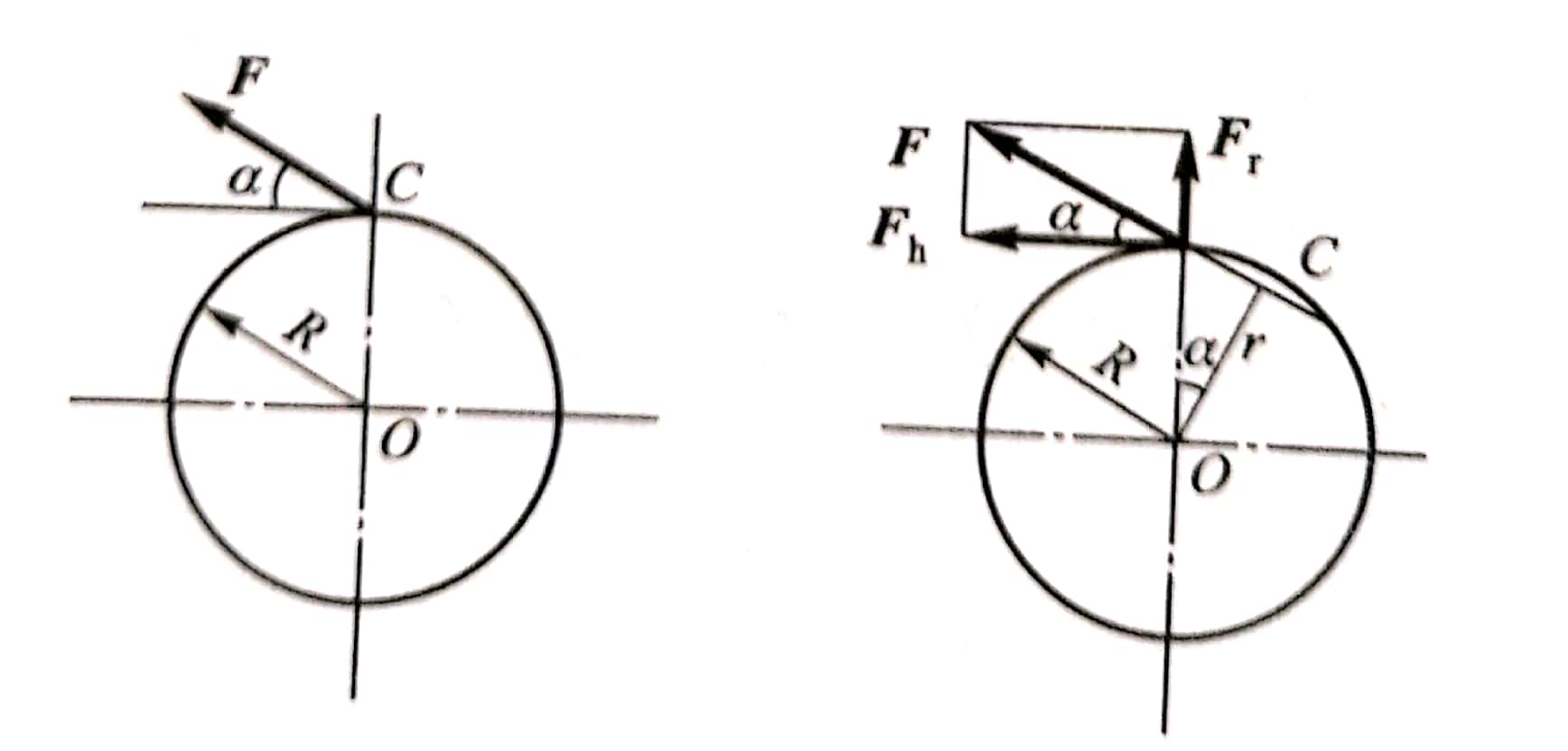
图2-14

解 计算力F对0点的矩，可直接利用定义求得，即

M₀(F)=r?F

因r=R?cosα，故

M₀(F)=F?R?cosα

根据合力矩定理，求得F对0点的矩。即将F分解为径向力F_r和水平方向力F_h，则

M₀(F)=M0(F_r) +M₀(F_h)

由于F_r过矩心0，则M₀(F_r)=0； 而F_h=F?cosα于是

M₀(F)=M₀(F_h)=F_h?R=F?R?cosα

由此可见，以上两种计算结果相同。

例2-4已知力F 的作用点A的坐标为x、y,如图2-15所示，外试求力F对坐标原点0的矩。

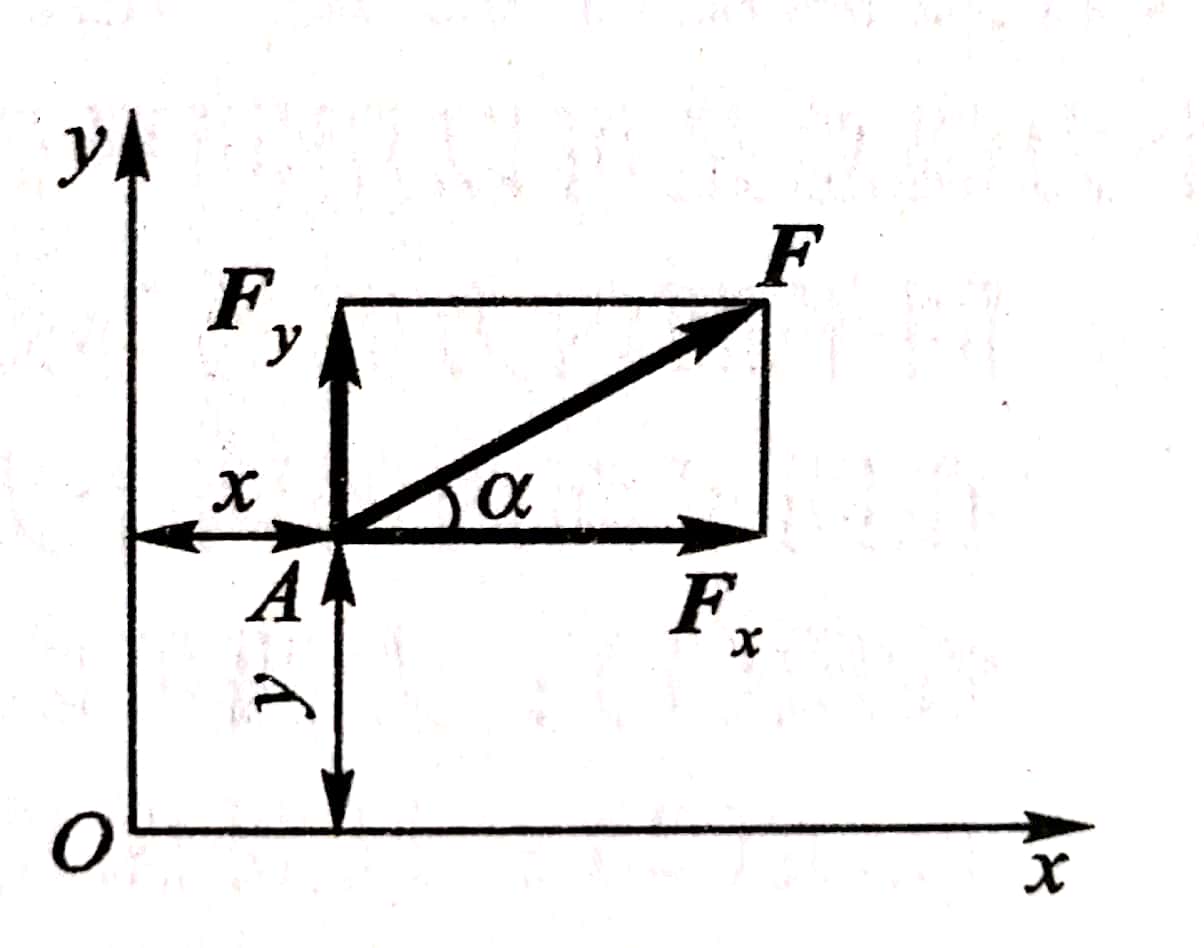
图2-15

解 由于本题力臂没有明确给定，直接应用力矩定义计算就比较麻烦，而利用合力矩定理进行计算就很方便，将力F沿坐标轴分解为两个分力F_x、F_y,则

M₀(F)=M₀(F_x) +M₀(F_y)

=Fy?x-Fx?y

            =F?x?sinα-F?y?cosα