在生产实践中，受到拉伸或压缩的杆件虽然外形各有差异，但构件都是直杆，因此在计算中都可以简化为图3-3所示的受力简图。

图3-3

由图3-3可见，杆件拉伸和压缩的受力特点是：作用于杆件上的外力合力的作用线沿杆件轴线。变形特点是：沿轴线方向产生纵向伸长或缩短。凡以轴向伸长为主要变形特征的杆件称为拉杆，以轴向压缩为主要变形特征的杆件称为压杆。但是仅确定了拉伸或压缩杆件的轴力还不能解决杆件的强度问题。因为同样的轴力，作用在不同大小的横截面上，会产生不同的结果。例如，用两根材料相同而截面尺寸不同的杆件做拉伸试验，使二者承受的轴力始终相同，随着外力的增加，则截面尺寸小的杆件首先被拉断。可见杆件的强度不仅与轴力有关，而且与截面尺寸有关。工程上常用单位面积上的内力来比较和判断杆件的强度。内力是连续分布在截面上的，应力描述了内力在截面上的分布情况和密集程度，它才是判断杆件强度是否足够的根据。

要确定应力，必须了解内力在横戴面上的分布情况。一般认为， 杆件横截面上的内力是均匀分布的。根据应力的定义和橫截面上应力均匀分布的规律，可以得到

    (3-1)

式中，σ—横截面上的应力：

F_N—横截面上的轴力：

A—橫截面面积。

式(3-1)即为轴向拉伸和压缩时横截面上应力的计算公式。由于分布在横截面上的内力皆垂直于截面，此时的应力也必然垂直于截面，这种垂直于截面的应力，称为正应力。当轴力为拉力时，为拉应力：轴力为压力时，为压应力。通常以正号表示拉应力；以负号表示压应力。

例3-2 圆截面杆如图 3-4a所示，已知F₁=400N，F₂=1000N, d=10mm，D=20 mm.试求圆杆横截面上的正应力。

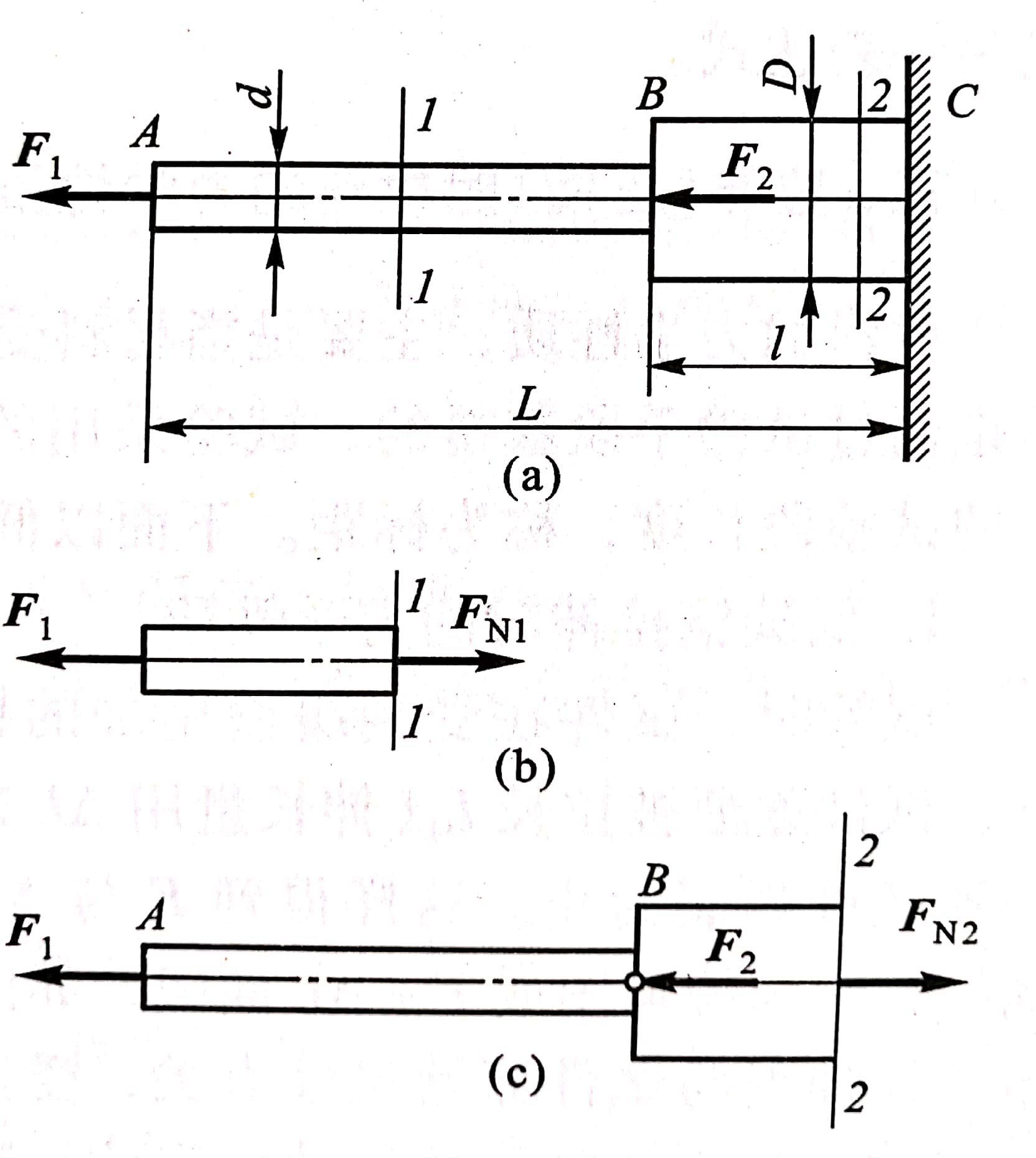
图3-4

解 由于该杆AB段和BC段的横戴面面积不同，所以正应力不相等，应分段计算。

(1)计算各段内的轴力

AB段：取1-1截而左段为研究对象，如图3-4b所示，列平衡方程式:

∑F_X=0，F_N1-F₁=0

F_N1=F₁=400N

BC段：取2-2截面左段部分，如图3-4c所示，

∑F_X=0，F_N2-F₁-F₂=0

F_N2=F₁+F₂=1400N

(2)计算各段正应力

AB段：

BC段：

当拉(压)杆受到轴力作用后，杆中横截面上的任-点都将产生正应力σ，同时该点相应产生纵向线应变ε。正应力σ表示为

σ=F_N/A

线应变ε为单位长度的伸长量。正应力σ与线应变ε存在下列关系：

σ=E ?ε    (3-2)

式中，E—比例系数， 称为弹性模量。在一定的范围内，一点处的正应力同该点处的线应变成正比关系。式中E的量纲与正应力σ的量纲相同，E的常用单位为MPa或GPa。式(3-2)称为胡克定律，适用于单向拉伸、压缩。

拉杆伸长量可用下式计算：

     (3-3)

式中，FN—轴力；

L—杆长；

E—弹性模量；

A—杆件的横截面积。

式(3-3)的应用条件为：在杆长L范围内，F_N 、E、A分别为常量。式(3-3)是胡克定律的另一表达式。