梁上各横截面内剪力为零、弯矩为常数时的弯曲变形，称为纯弯曲。

在梁表面画上均匀的横线和纵线，然后在梁的纵向对称面内施加一对力偶M(图3-32)。观察梁的弯曲变形可知:

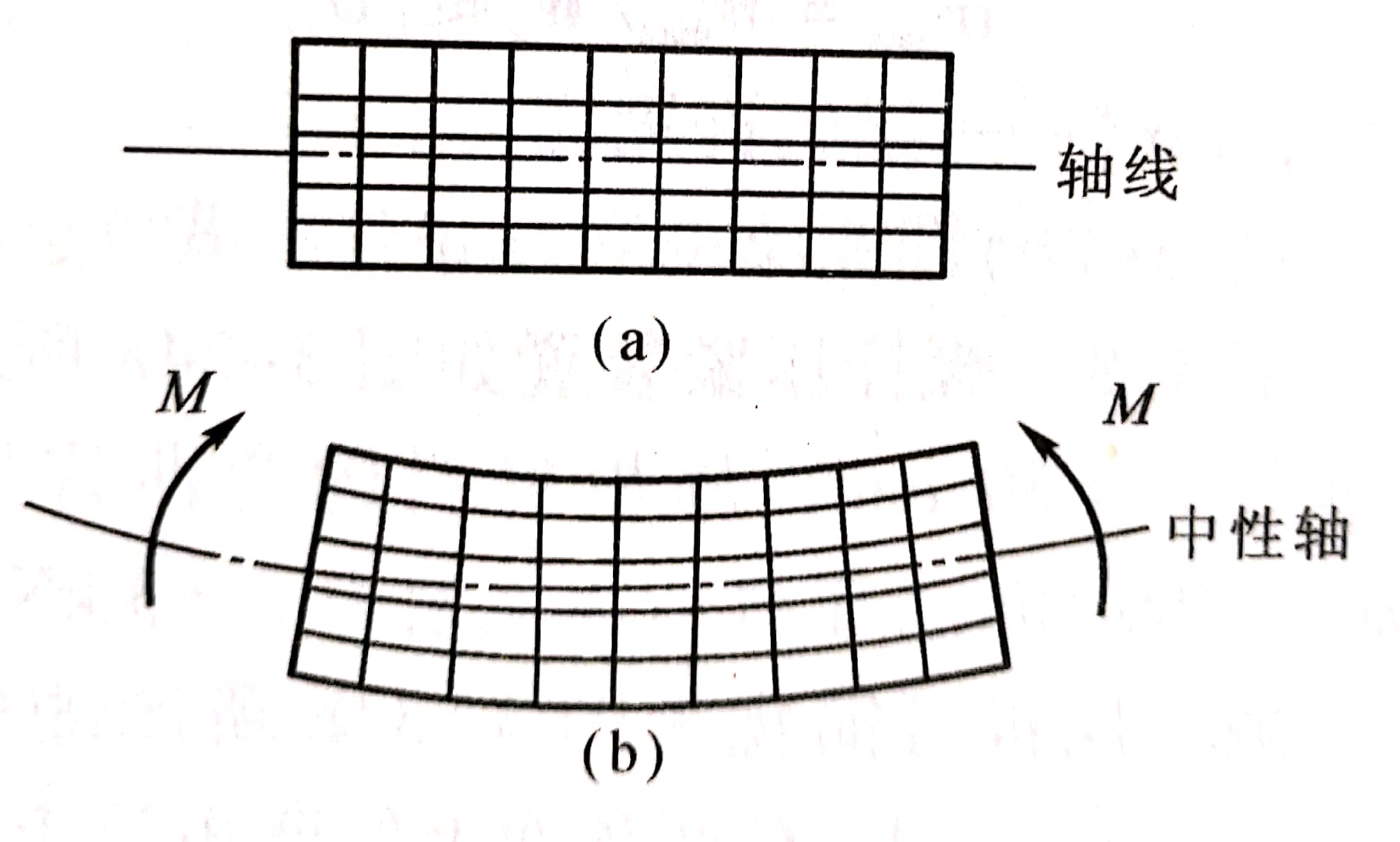
图3-32

(1)横线仍为直线，且仍与纵线正交，但转了一个角度。

(2)所有纵线变为圆弧线，梁上部凹边纵线缩短，下部凸边纵线伸长。

因此，可以假想梁是由无数根纤维组成，梁下部纤维伸长是由于受拉所致，上部凹边缩短为受压所致。各纤维之间相互挤压，而在受拉区(下部)和受压区(上部)之间存在一层既不伸长也不缩短的纵向纤维层，称为中性层。中性层与横截面的交线称为中性轴。弯曲变形时，横截面绕中性轴旋转。在纯弯曲时，横截面上每点处的应力与变形(伸长或缩短)情况和轴向拉、压时的情况相同。在梁上部凹边压缩最大，压应力最大；梁下部凸边拉伸最大，拉应力也最大；因中性层既不伸长也不缩短，所以中性层的正应力为零。由此可见，梁的横截面上任意点的正应力与该点到中性轴的距离成正比(图3-33)。

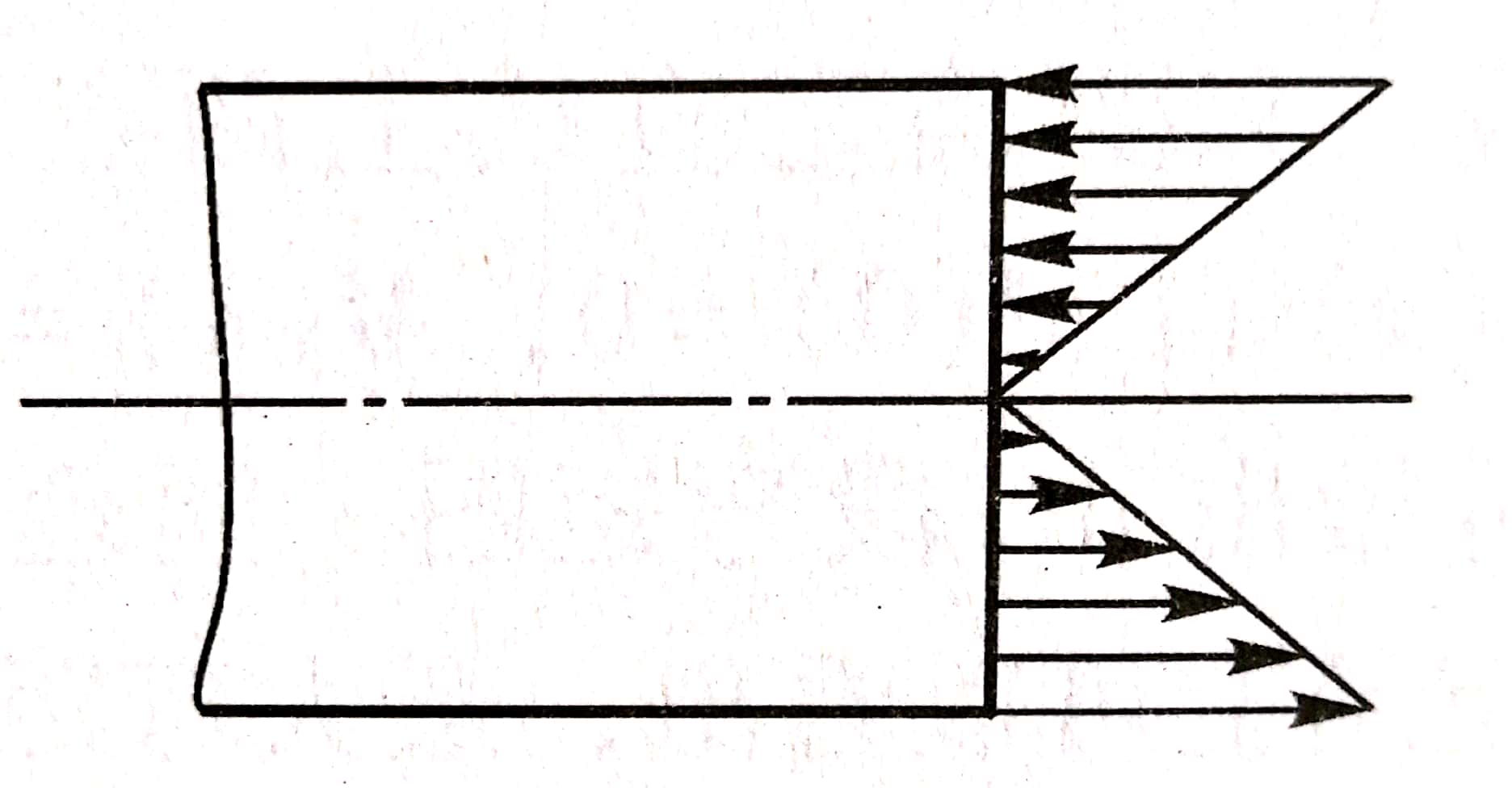
图3-33

弯曲正应力计算公式为

    (3-24)

式中，σ—橫截面上任一点处的弯曲正应力；

M—该横截面上的弯矩；

y—该点到中性轴的距离；

I—该横截面对中性轴的截面二次矩。

当式(3-24)中y取最大值y_max (即横截面上、下边缘)时有最大正应力：

令

    (3-25 )

式中，W_z—抗弯截面系数。

为保证梁安全可靠，应使梁的最大正应力不超过梁的许用正应力，即

     (3-26)

式中，[σ]—梁的许用应力。

式(3-26)即为梁的强度条件公式。

例3-9 螺栓压紧装置如图3-34a所示。已知板长a =50 mm，压板材料的弯曲许用应力[σ] =160 MPa，工件所需夹紧力F=3kN,试校核压板的强度。

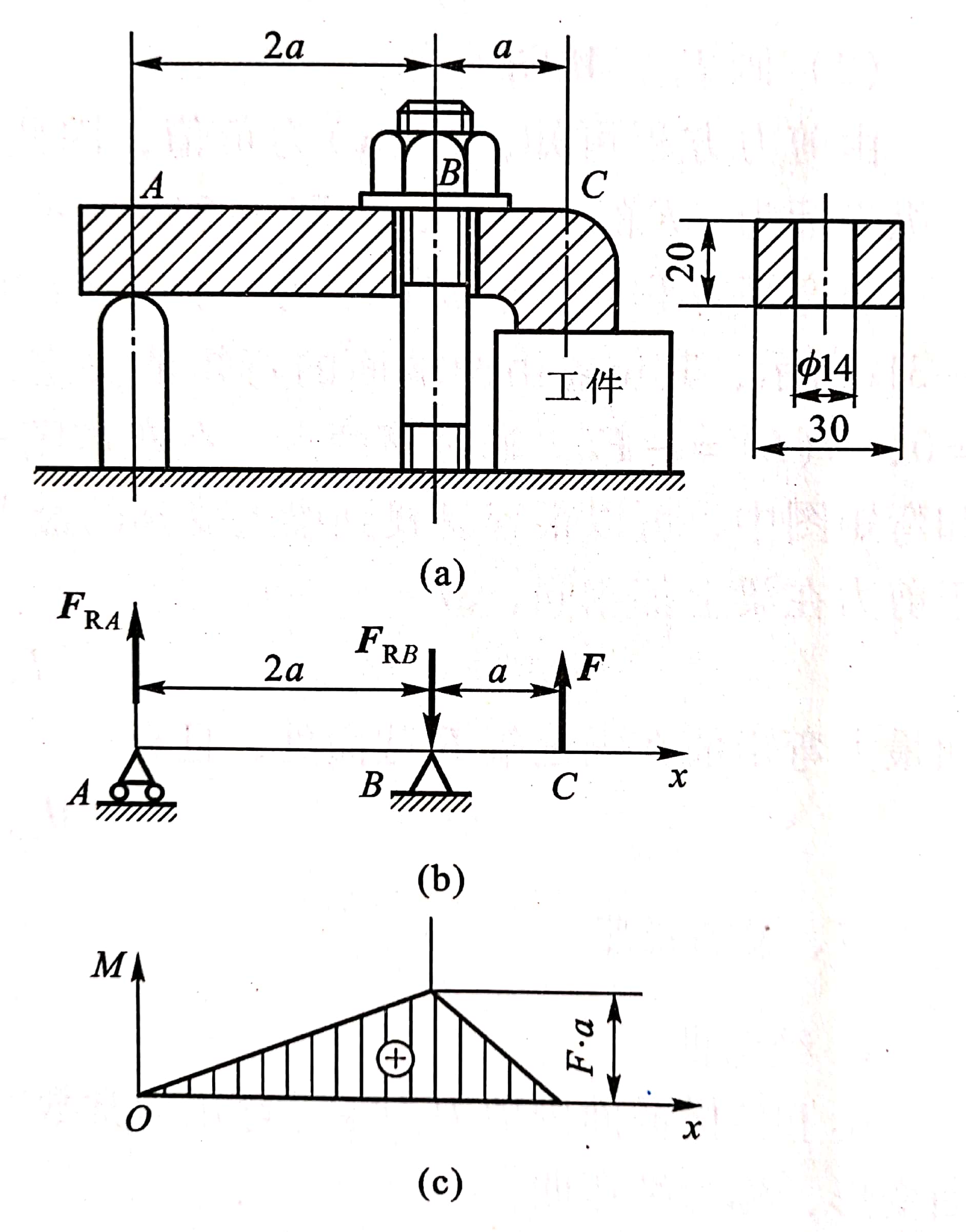
图3-34

解 压板可简化为图3-34b所示的外伸梁。由梁外伸部分BC可以求得截面B的弯矩M_B=F ? a，而A、C两截面上的弯矩等于零，弯矩图如图3-34c所示。由弯矩图可知，B截面上弯矩最大，且M_max =M_B=F ? a=150N?m。

根据截面B的尺寸可求得:

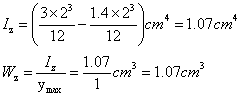
根据抗弯强度条件公式得

由此可知，螺栓压板有足够的强度。