设在刚体上作用有力F₁， F₂ ，…， F_n ，使刚体处于平衡状态(图2-22a)。在力的作用面内任选一点0,将作用于刚体上的各力F₁， F₂ ，…， F_n 平移到点0,并产生附加力偶组成的力偶矩M₁，M₂，…，M_n。

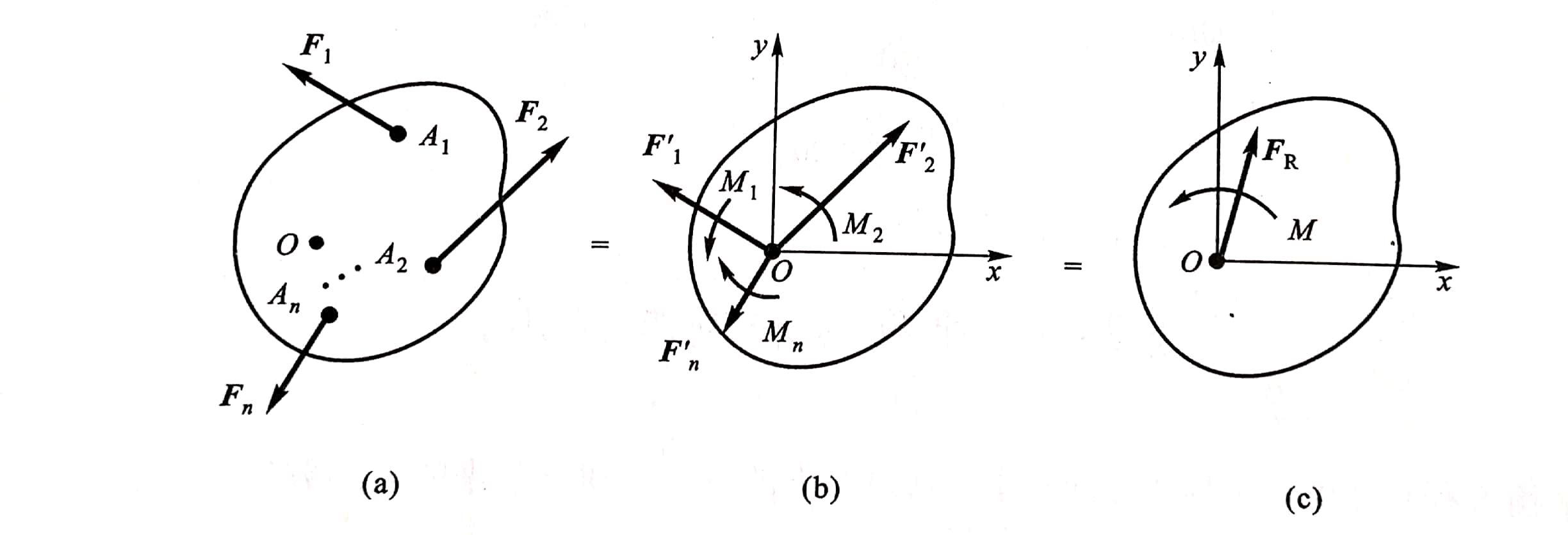
图2-22

若使刚体处于平衡，则必领满足作用于刚体上的合力矢F_R=0，合力偶矩M=0，即

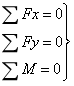    (2-6)

例2-5 图2-23a 所示为装载混凝土翻斗车车斗，车斗及混凝土共重w=5kN,为防止重心偏移自动翻斗卸料，在A点处用挂钩锁住，如水平锁住力为F,方向为水平向右，已知BO_y的距离为0.1m，AO_x的距离为0.5m,求0点处的反力及A点处的水平锁住力F。

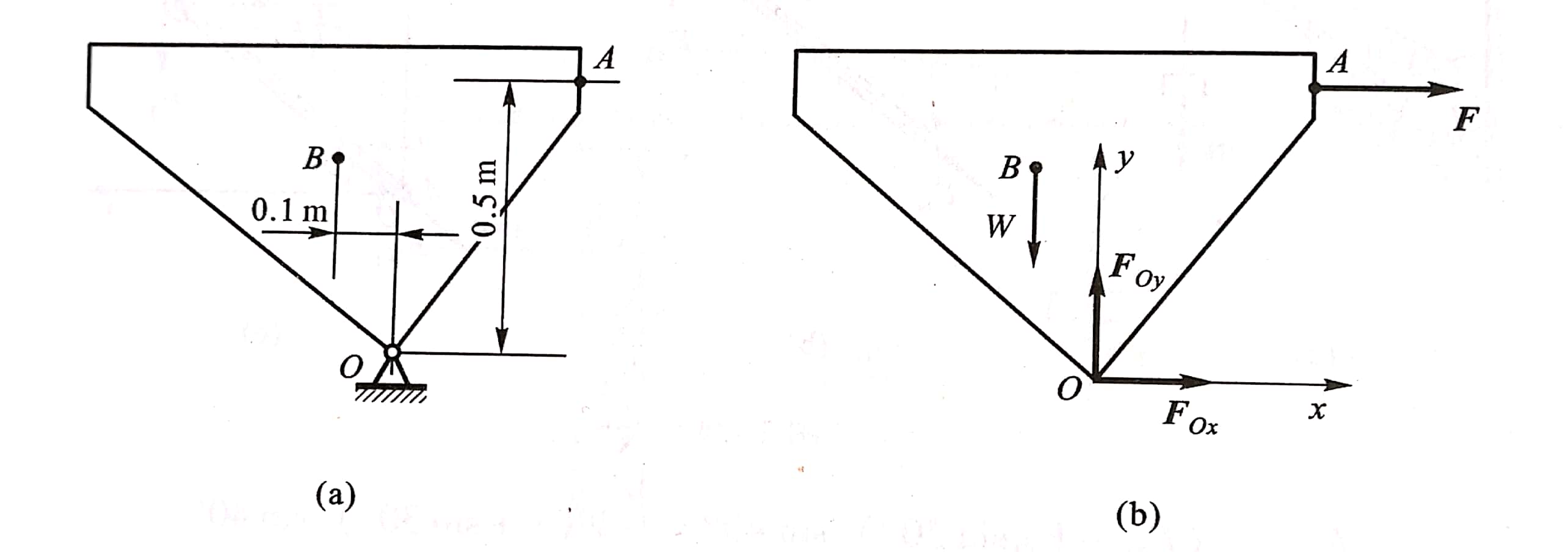
图2-23

解  翻斗车的车斗处于平衡状态， 其受力如图2-23b所示，支点0处受反力为F_ox、 F_oy，方向如图。取0点为坐标系原点，列出平衡方程为:

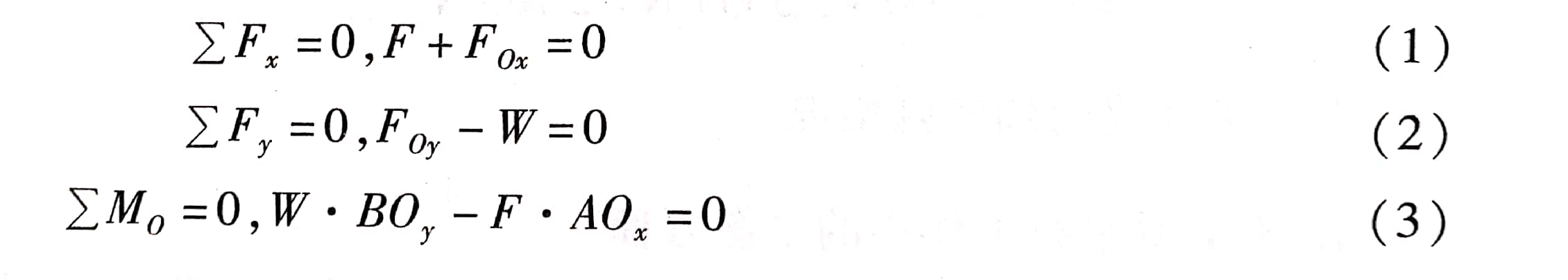
由式(2)，直接求出

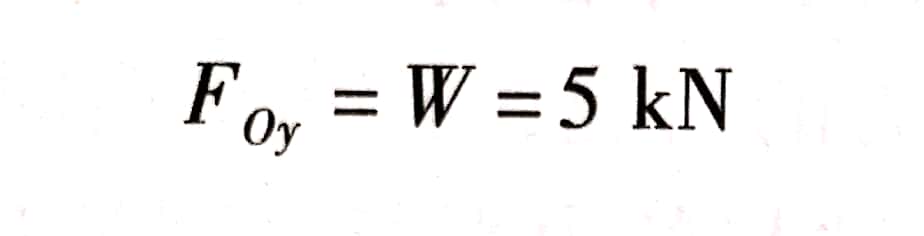
由式(3)直接求出

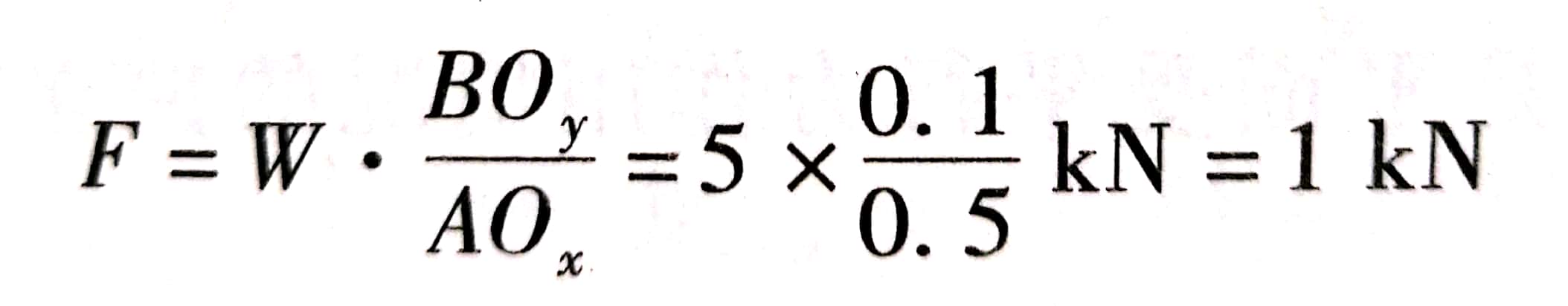
以此值代入式(1)，即得

说明实际0点的x方向受到的反力F_ox与图中标注方向相反，即应向左。

例2-6 简易起重机起重臂AB的A端安装于固定铰链支座，B端用水平绳索BC拉住，起重臂与水平线成40°角，起重臂在B端装有滑轮，钢丝绳绕过滑轮把重量w =3000 N的重物吊起，钢丝绳绕过滑轮前与水平线成30°角(图2-24a)。设起重臂自重略去不计，求平衡时支座A和绳索BC的反力。

解 以起重臂AB连同滑轮作为研究对象。画出它的受力图(2-24b)。起重臂受到的力有:滑轮两边钢丝绳的拉力F_T1、F_T2。如果不计摩擦，F_T1=F_T2=W=3000N; 绳索BC的拉力F_T3；支座A的反力F_N，因为F_T1和F_T2的大小相等，它们的合力必通过B点，所以F_T1和F_T2可认为作用在点B。由于起重臂只在A、B两点受力，是个二力杆，故反力F_N必沿连线AB。在受力图上以A为直角坐标系0xy的原点，如图2-24c 所示，列出平衡方程:

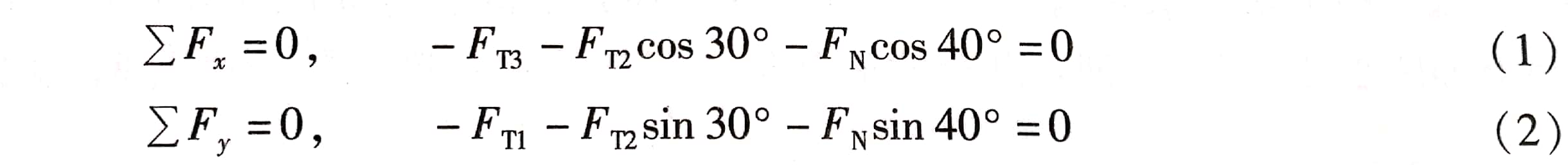
已知F_T1=F_T2=W=3000N,只有F_T3、F_N是未知量，由式(2)求得

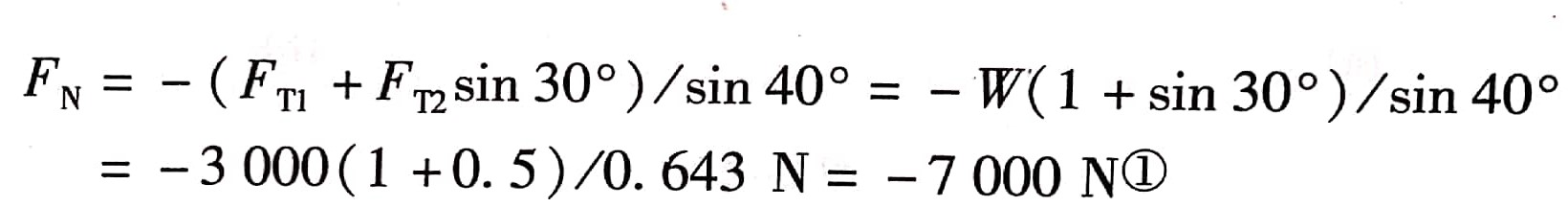
把F_{N=-7000N代入式（1）得到}

①F_N值求得后为负值，说明其方向与图示假设方向相反；如求得值为正值，说明其方向与图示假设方向相同。