力是矢量，如果当力的作用线在刚体上平行移动时，它对刚体的作用效果就会改变。那么要使力的作用线在刚体上平移又不改变对刚体的作用效果，就必须有附加条件，这就是力的平移定理所要解决的问题。

1.力的平移定理

定理:可以把作用在刚体上点A的力F平行移到一点B，但同时必须附加一个力偶，这个附加力偶的矩等于原来的力F对新作用点B的矩。

证明:图2-19a中力作用于刚体的点A。在刚体上任取一点B， d为点B至力F作用线的垂直距离，在点B加上两个等值反向的力F'和F″，并使F=F'=F″，显然三个力F、F'、F″组成的新力系与原力等效，如图2-19b所示。此时可将F'看作是力F平移到点B后的力，而F、F″构成一力偶。该力偶就是所需的附加力偶。如图2-19c所示，附加力偶矩为

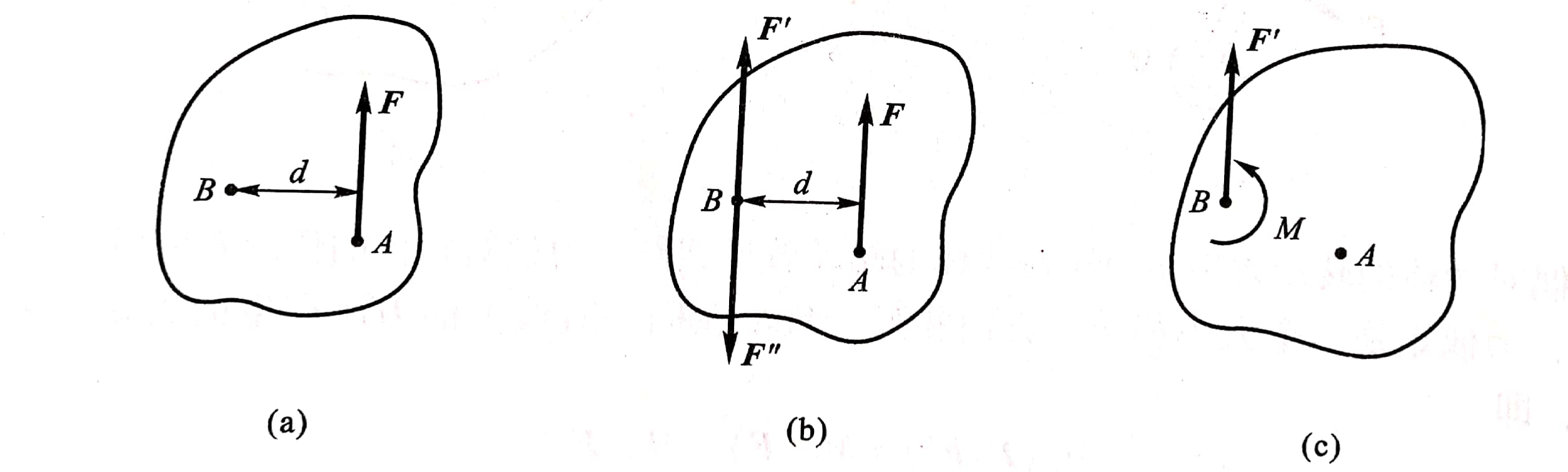
图2-19

M=F×d=M_B(F)     (2-4)

于是定理得证。

2.应用

由力的平移定理可知，可以将一个力答换成同平面内的一个力和一个力偶；反之，同一平面内的一个力和一个力偶也可以用一个力来等效替换。力的平移定理不仅是力系向一点简化的依据，也可解释一些实际问题。例如:如图2-20b所示攻螺纹时，必领用双手均匀握住扳手两端，而且用力要相等，不能只用一只手扳动扳手。因为作用在扳手AB一端的力F与作用点0的一个力F'和一个力偶矩M等效(图2-20a)。这个力偶使丝锥转动，而力F'却易使丝锥产生折断。

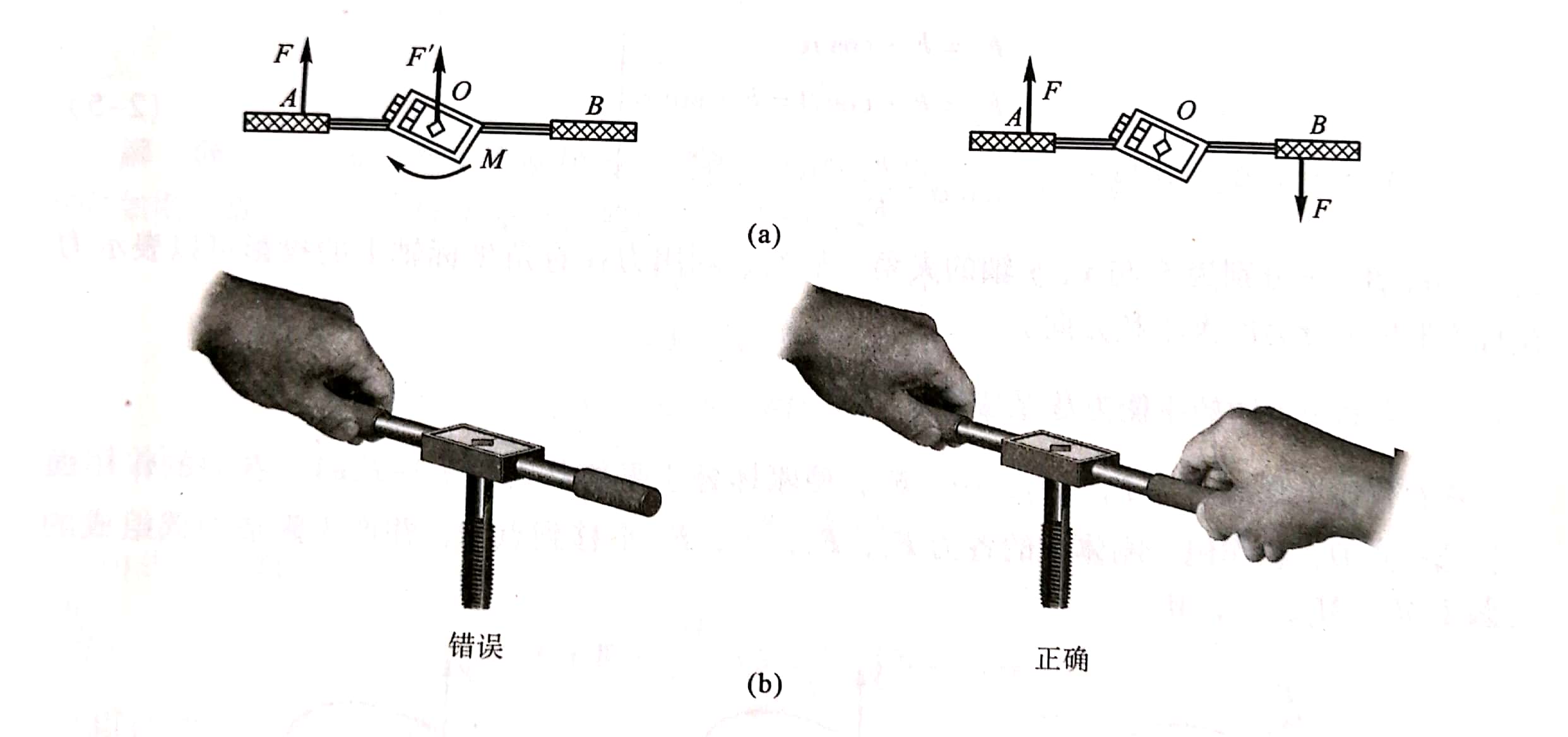
图2-20