梁的支承和受力很复杂，计算中常将梁简化为三种典型形式：

(1)简支梁

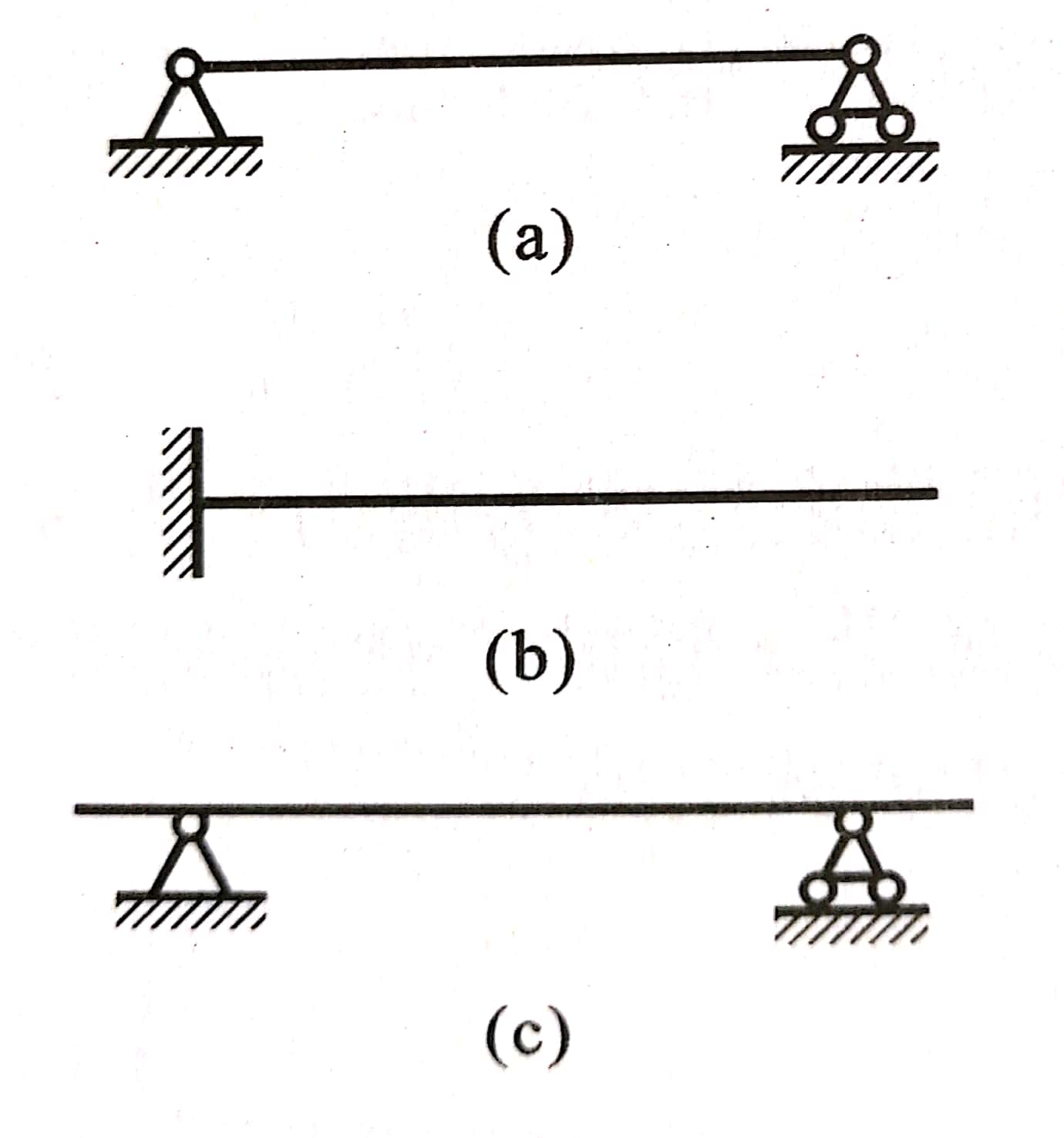
一端固定铰支承，另一端可动铰支承的梁，如图a所示。

(2)悬臂梁

一端固定铰支承，另-端自由的梁，如图b所示。

(3)外伸梁

具有一个或两个外伸部分的梁，如图c所示。

梁的内力包括剪力F_Q和弯矩M,下面以简支梁(图3-28)为例加以说明。

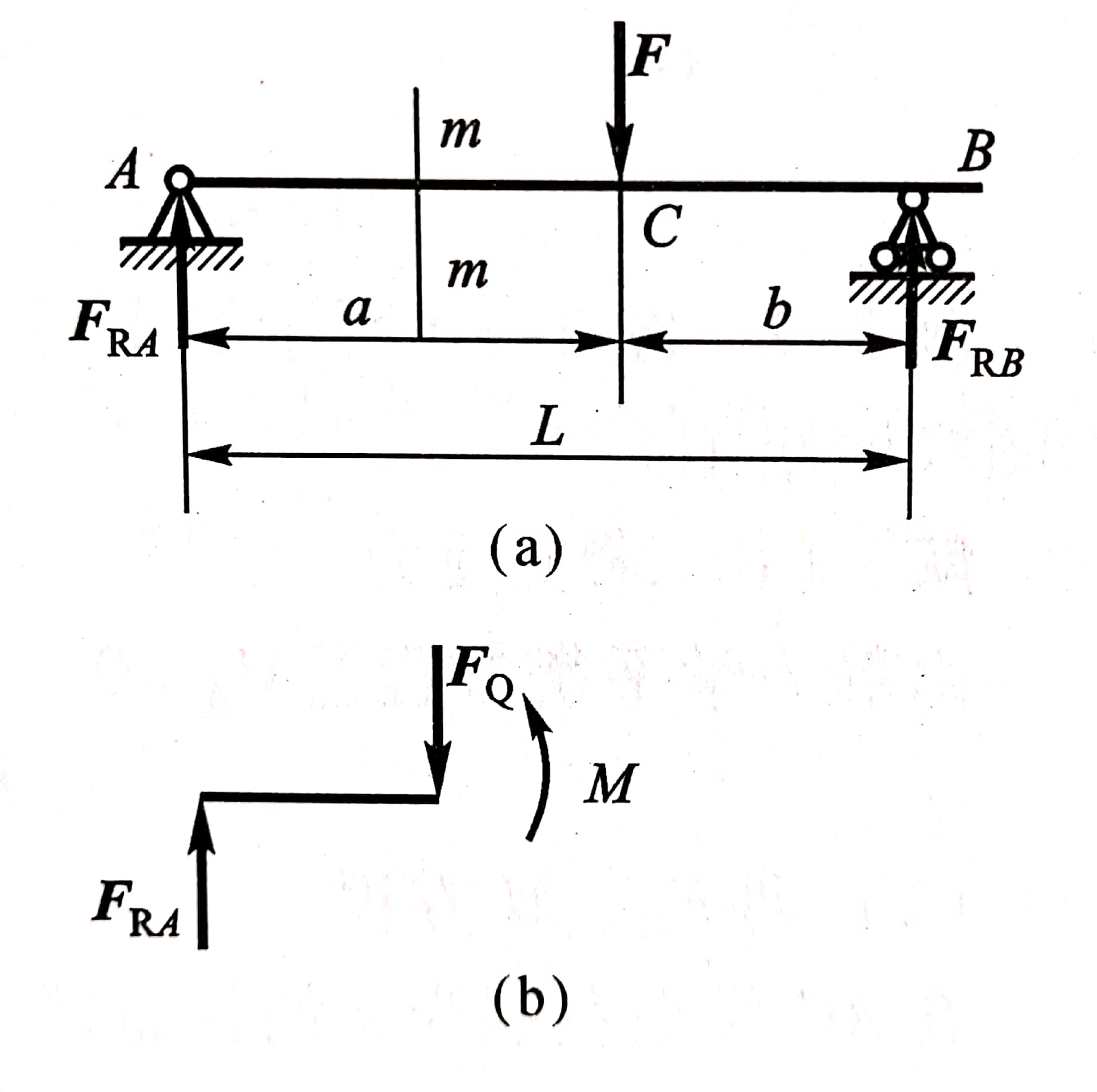
图3-28

1.首先求出梁上所受外力

F_RA=F ? b /L

F_RB=F ? a/L

2.用截面法求内力

①在截面m-m处假想地把梁切为两段。

②取左段为研究对象。由于左段作用着外力F_RA，则在截面上必有一与F_RA大小相等、方向相反的力F_Q。由于该内力切于截面，因此称为剪力。又由于F_RA与F_Q形成一个力偶，因此在截面处必存在一个内力偶M与之平衡，该内力偶称为弯矩。

③建立平衡方程：

由∑F =0，得：F_RA-F_Q=0，F_Q=F_RA

由∑M=0,得：M=F_RA ?  x

由此可以看出：弯曲时，梁的横截面上产生两种内力：一个是剪力，一个是弯矩。

3. 剪力和弯矩符号的规定(图3-29)

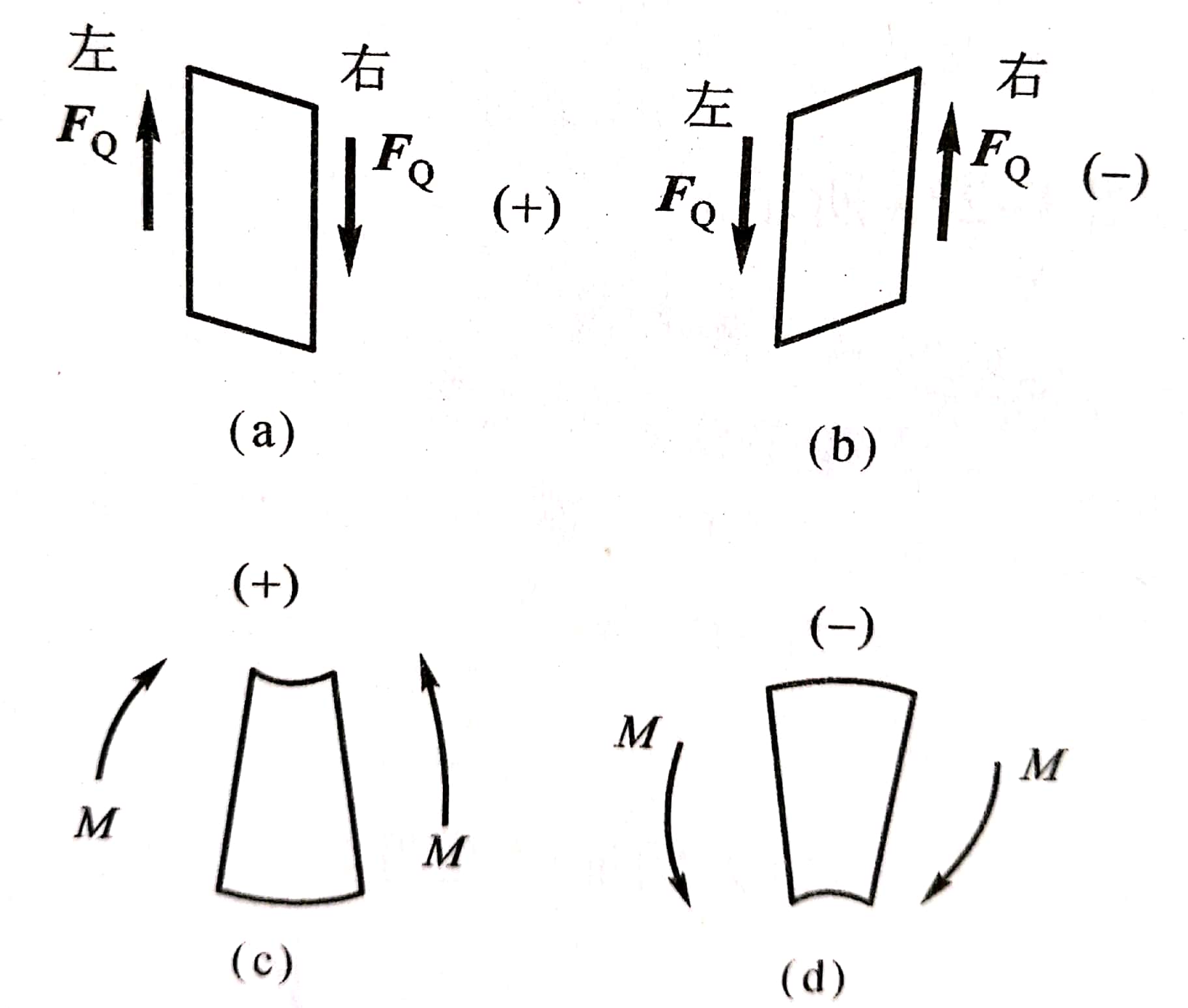
图3-29

剪力符号规定：左上、右下为正，反之为负。

弯矩符号规定:使梁弯段上凹为正，反之为负。

4.建立剪力、弯矩方程，绘制剪力、弯矩图

一般情况下，在梁的不同截面上，剪力F_Q和弯矩M是不相同的，并随着横截面位置的不同而改变。若以横坐标x表示横截面在梁轴线上的位置，则剪力和弯矩皆可表示为x的函数，即

F_Q=F_Q(x)，M=M(x)     (3-23)

上面的函数表达式为剪力、弯矩方程。

把F_Q、M沿x轴的变化情况用图线在坐标内表示出来，所得到的图分别称为剪力图和弯矩图。下面以实例来说明。

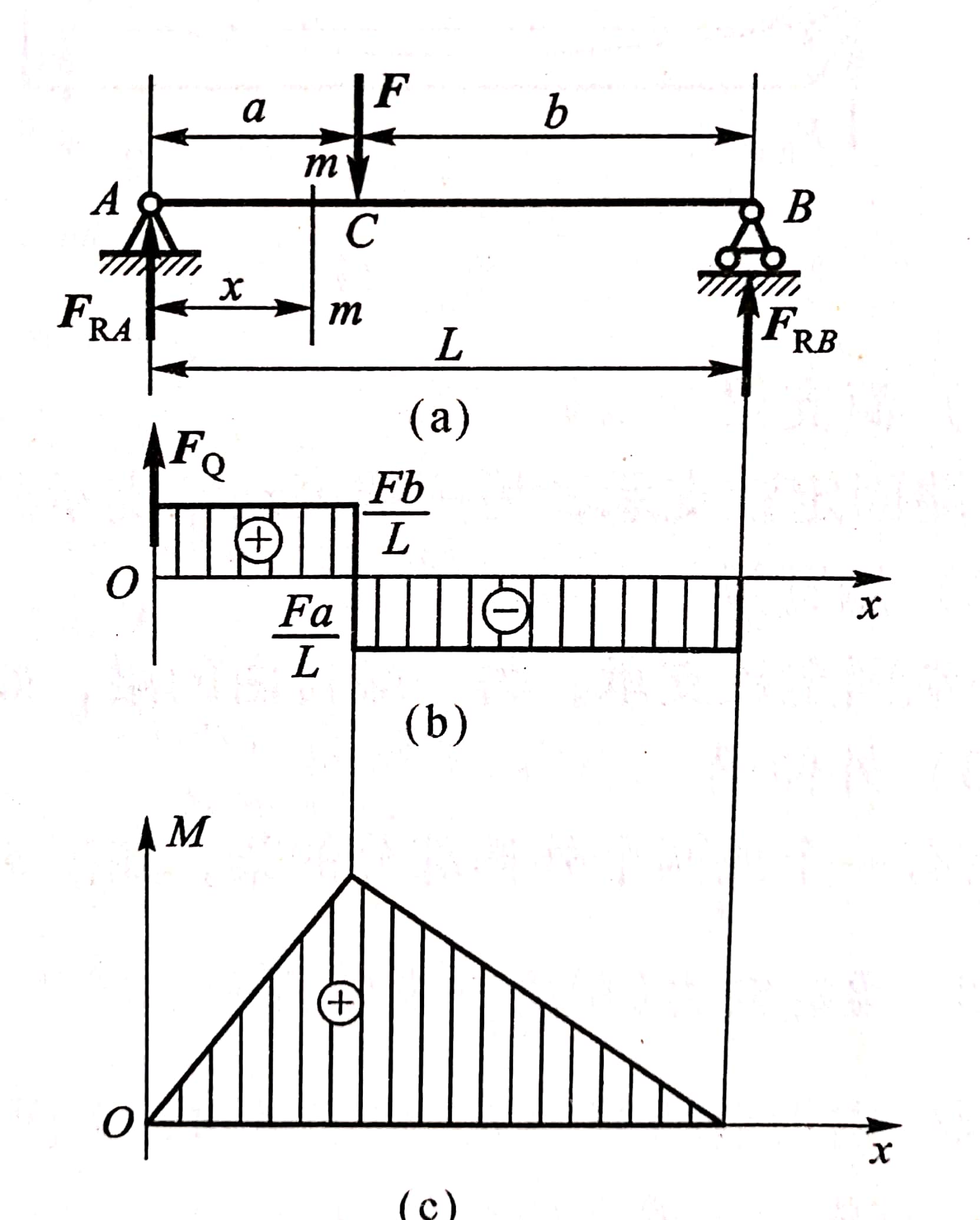
图3-30

例3-7 图3-30 所示简支梁受集中力F作用。试列出它的剪力方程和弯矩方程，并作剪力图和弯矩图。

解  (1) 求支反力

由静力学平衡方程∑M_B=0，∑M_A=0，可知：

F_RA=F ? b /L，F_RB=F ? a/L

(2)列F_Q、M方程

在AC段距左端为x的任意截面m- m处将梁截开，由于左端只有F_RA,则该截面上的F_Q、M分别为:

F_Q(x)=F_RA=F ? b /L， (0<x<a)

M(x)=F_RAx=F ? b ? x/L, (0≤x≤a)

如在CB段内取距左端为x的任意横截面，截面以左有F_RA和F两个外力，截面上的剪力和弯矩方程为:

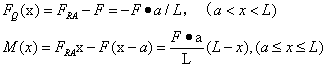
(3) 作F_Q、M图

在AC段，梁的任意横截面上的剪力F_Q为常数F ? b /L，符号为正，即剪力图为在x轴上方且平行于x轴的一条直线。同理，BC段也平行x轴，由于F_Q值为负，直线在x轴下方。从剪力图可看出，当a<b时，最大剪力为

|F_Qmax| =F ? b /L

在AC段，弯矩是x的一次函数，弯矩图为一条斜线，只要确定直线上两点即可确定。由M(x) = F_b/L(x)得M(0)=0, M(a)=F ? a ? b/L，于是过此两点可做出AC段弯矩图。同理可画出CB段弯矩图。从弯矩图上可以看出，最大弯矩发生在截面C.上，即

|M_max| =F ? a ? b/L

例3-8 悬臂梁 AB如图3-31a所示，在自由端A处作用有集中载荷F,试画出此梁的剪力图和弯矩图。

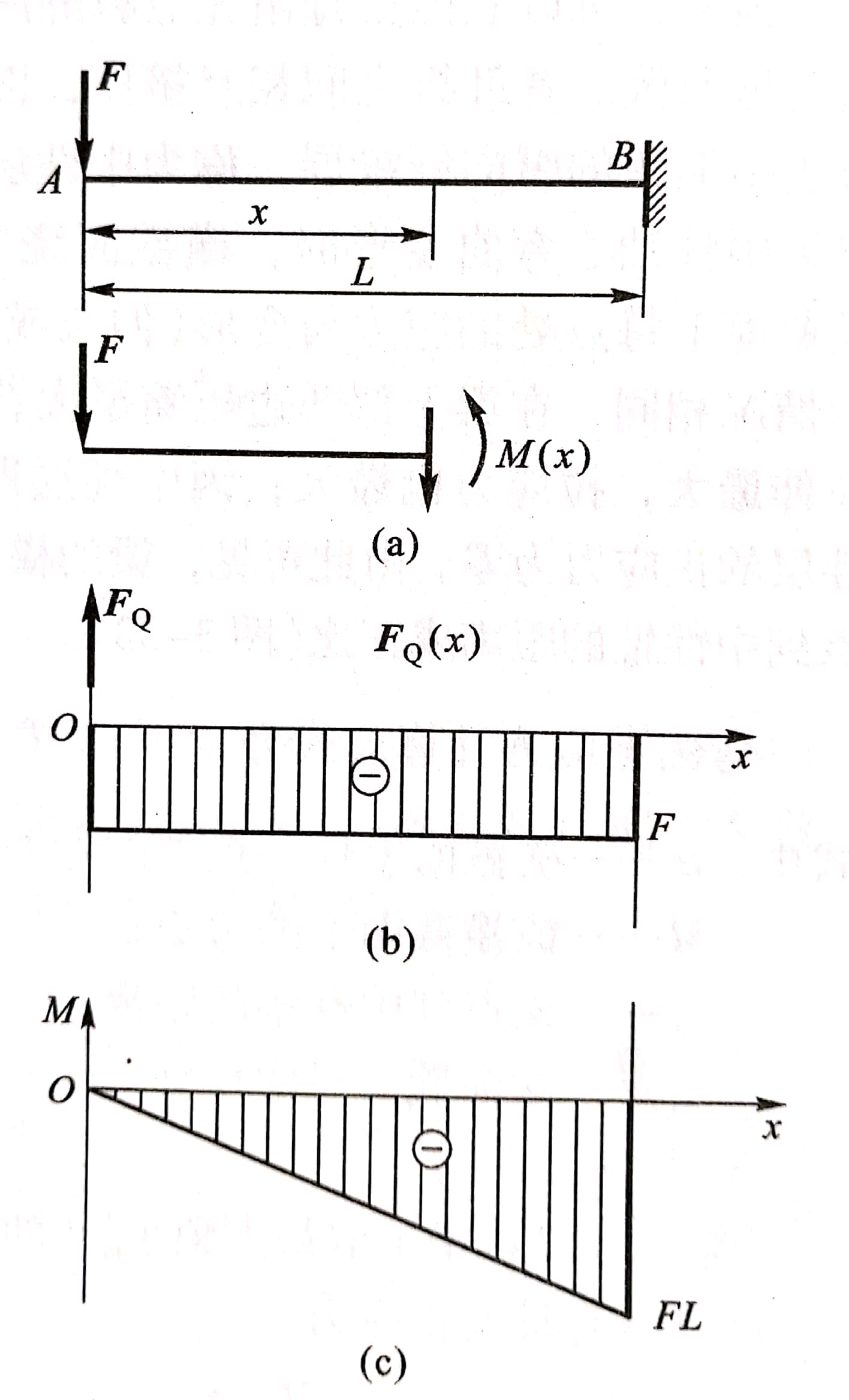
图3-31

解 (1) 列剪力方程和弯矩方程

在梁上任意截面左端x处将梁截断，取左侧为研究对象。由于左侧只有一个外力F作用，于是剪力方程和弯矩方程为:

F_Q(x)= -F

M(x)= -F ? x

(2) 画F_Q、M图

由剪力方程可知，F_Q(x)为负值，因此，F_Q图为一纵坐标为-F的水平线，如图3-31b所示。

由弯矩方程可知: M(x)为x的一斜直线，如图3-31c所示，其位置由两端面的弯矩值决定，即M(0)=0，M(L)= -FL。通过该两点，在弯矩图坐标系中连线，则该斜线即为梁的M图。在剪力和弯矩图中，可以很容易找到梁上受到的最大剪力值和弯矩值，从而找到弯曲受力危险点。由于剪力在梁上都相同，故

|F_Qmax| =F 

而最大弯矩值在固定端B截面处，且有

|M_max| =F ? L