1.扭转现象与假设

如图所示，在圆轴的表面上画出很多等距的圆周线和轴线平行的纵向线，形成大小相等的矩形方格。当圆轴扭转变形时，可以看到：

①各圆周线相对于轴线旋转了一个角度，但其形状大小及圆周线间距没有变。

②各纵向线，均倾斜了一个小角度，矩形变成了平行四边形。

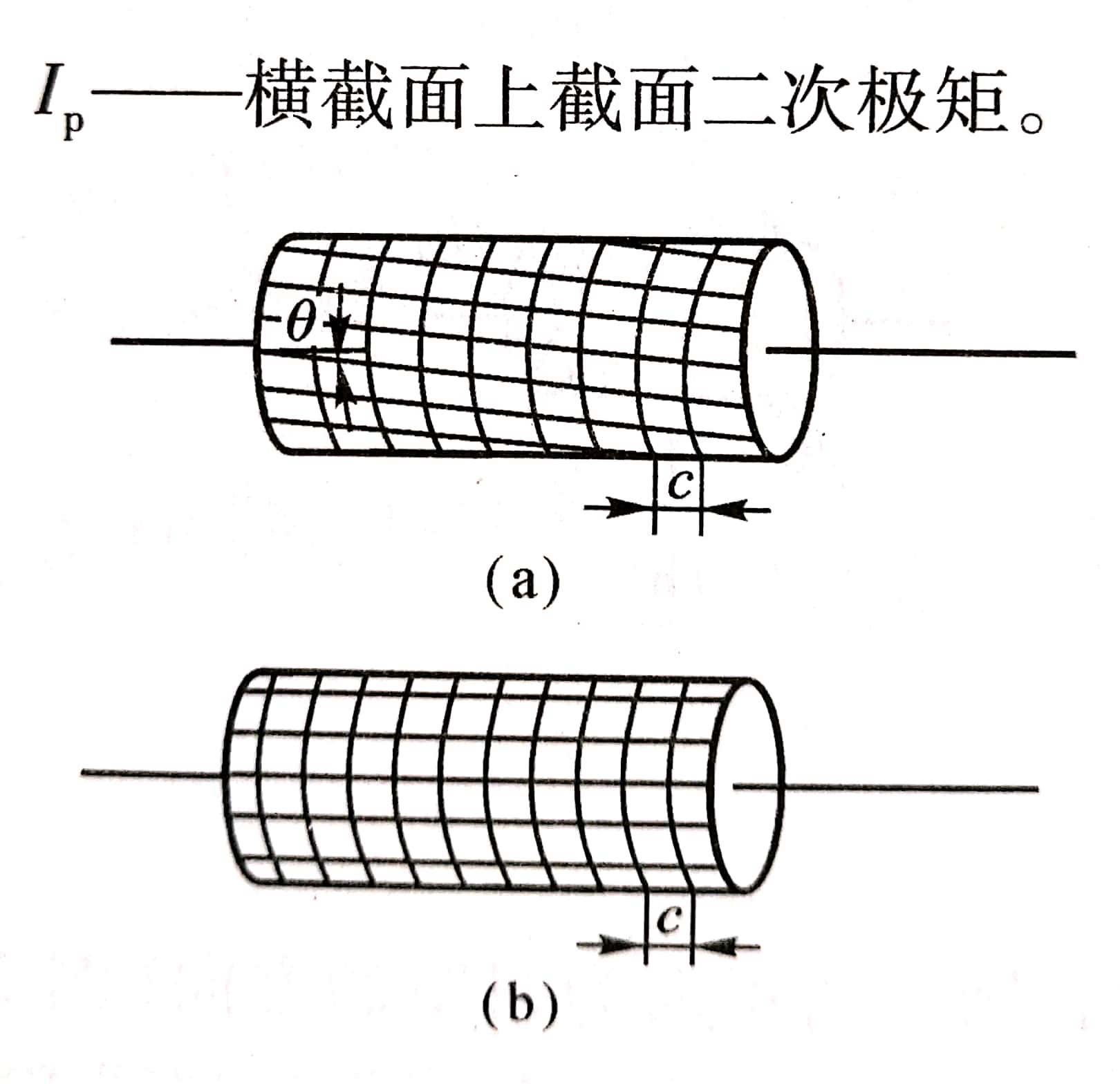
由以上的观察，可得出圆轴扭转时的基本假设：

扭转时，圆轴的横截面始终为平面，形状、大小都不改变，只有相对轴线的微小扭转变形，因此在横截面上无正应力，而只有垂直于半径的切应力。

2.切应力分布规律

圆轴横截面上任一点的切应力与该点所在圆周的半径成正比，方向与过该点的半径垂直，

切应力最大处发生在半径最大处。应力分布规律如图所示。

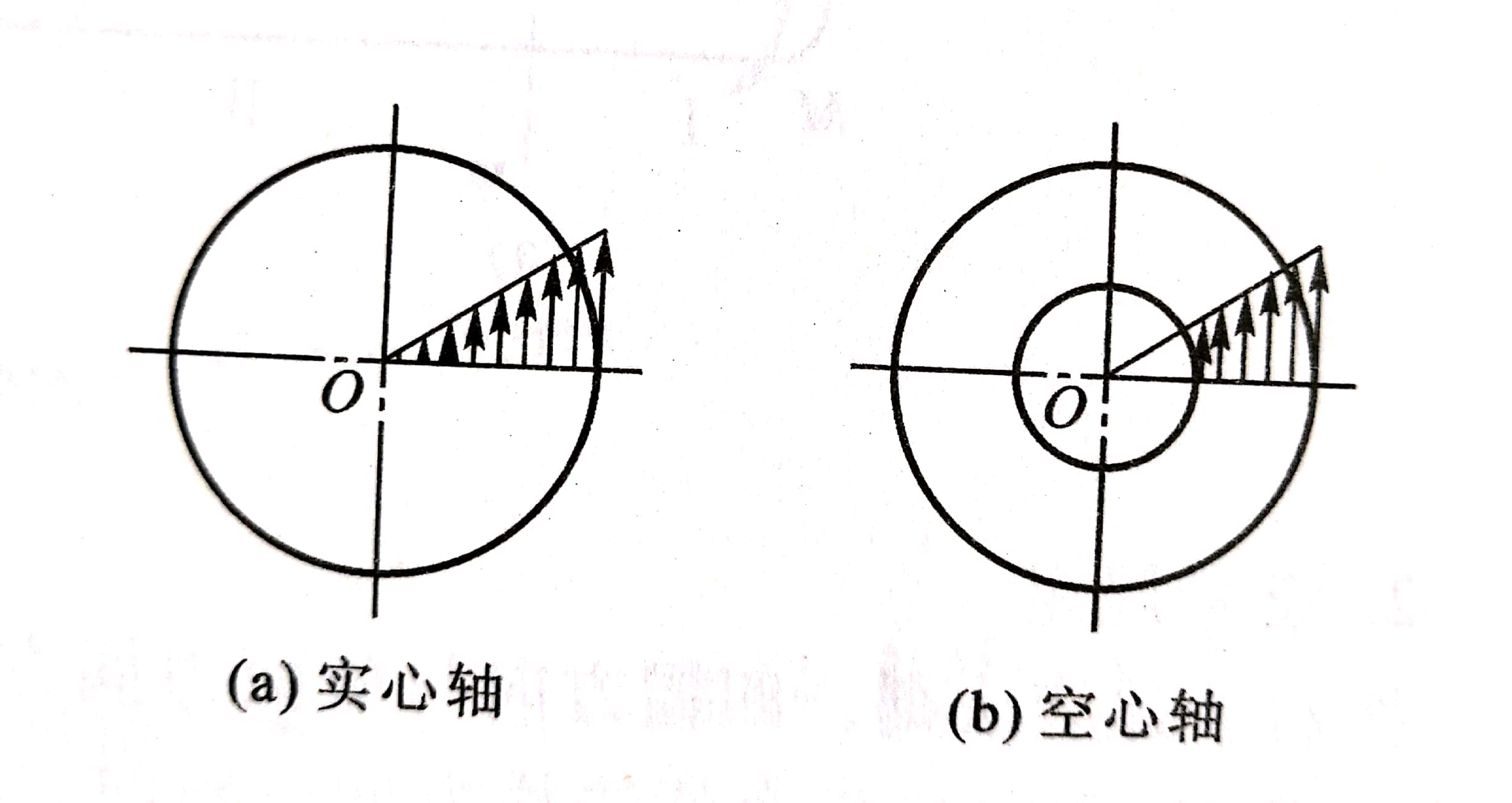
3.切应力计算公式

根据静力学关系导出切应力计算公式为

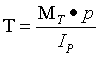
Ρ——横截面上任意一点的半径；

I_P——横截面上截面二次极矩。

当ρ=R时，切应力最大，即

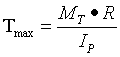
令I_P/R=W_t，于是上式可改写成：

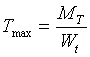
式中，W_t——抗扭截面系数。

4. I_P和W_t的计算

(1)实心圆轴

截面二次极矩：

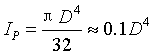
抗扭截面系数：

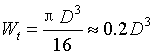
(2)空心圆轴

截面二次极矩：

I_P=0.1D⁴(1-α⁴)

抗扭截面系数：

W_t=0.2D³(1-α⁴)

式中，α=d/D。