构件受力时，有时各力作用线在同一平面内并相互平行，如图2-25所示。起重机、桥梁等结构上所受力常常可简化为平行力的情况，且其平衡时也应满足平面受力的平衡方程。如选择0y轴与各力平行，则∑F_x =0就成了恒等式而不再有用了，于是平面受平行力作用情况的独立方程只有两个，即也可以表示为两力矩形式，即

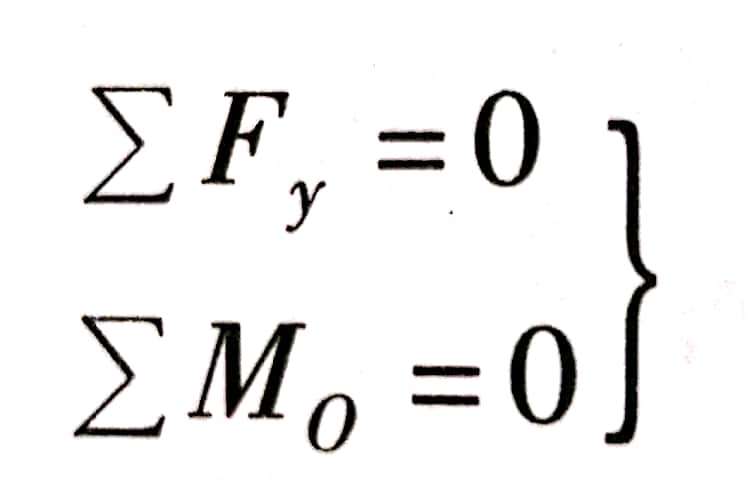    （式2-7）

也可以表示为两力矩形式，即

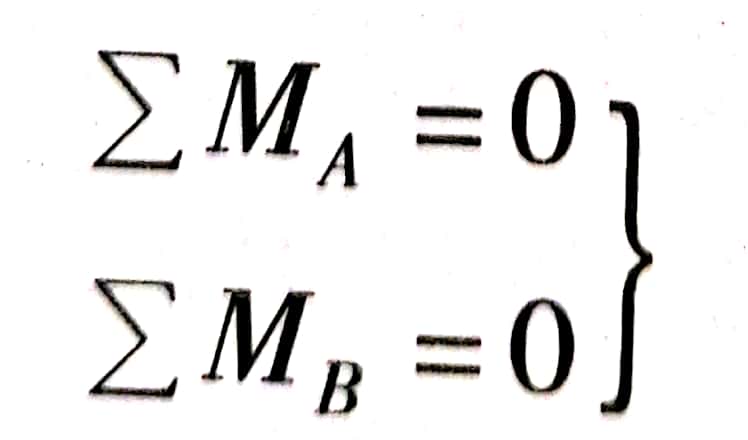    （式2-8）

但AB连线不能与诸力平行。

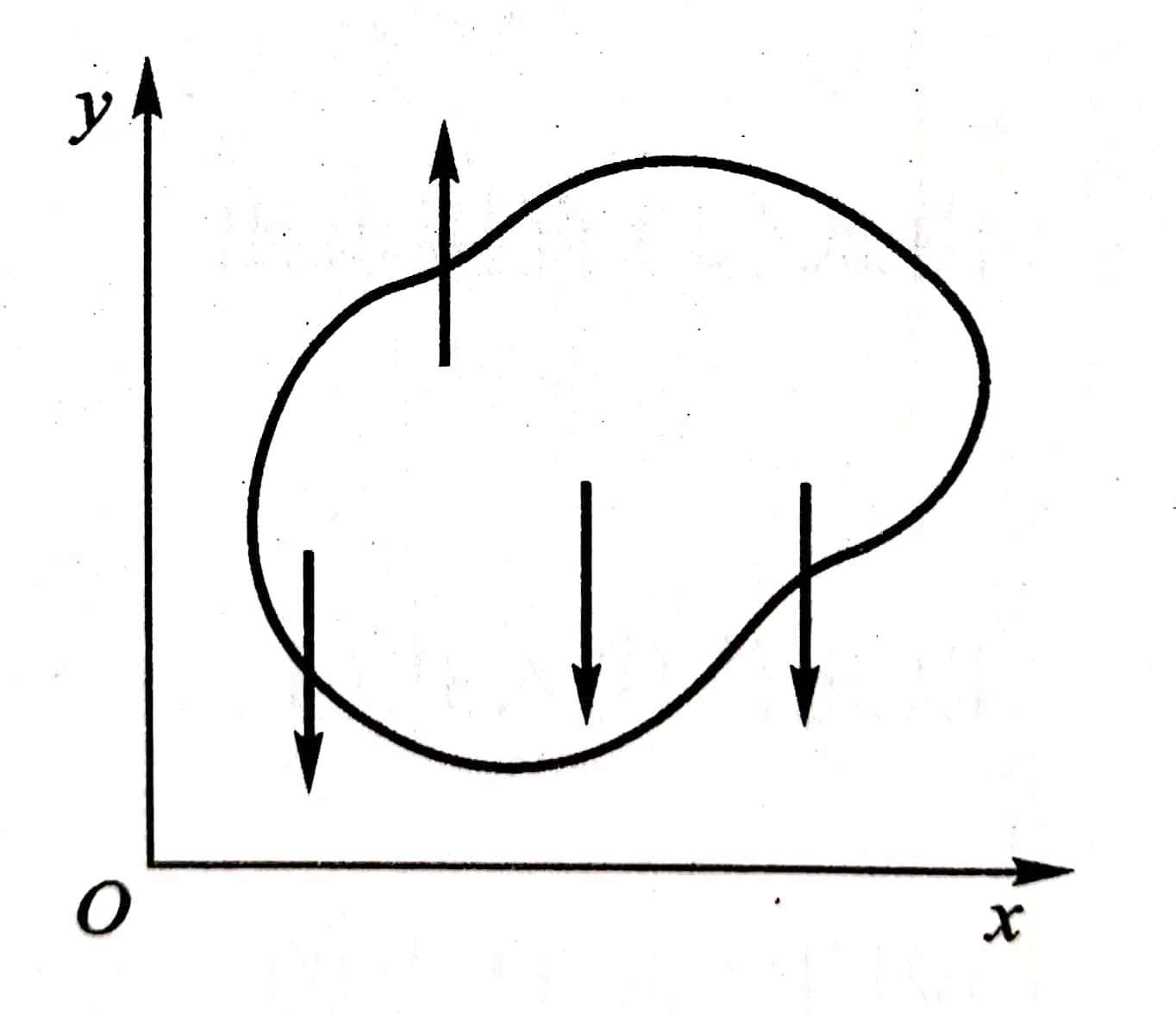
图2-25

例2-7 塔式起重机如图2-26 所示。机架重W₂ = 700 kN，作用线通过塔架的中心，最大起重量W₁ =200kN,最大悬臂长12m，轨道A、B的间距为4m，平衡块重W₀ 到机身中心线距离为6m，试求:

(1)保证起重机在满载和空载时都不致翻倒时平衡块的重量W₀ 。

(2)平衡块重W₀ =180kN, 满载时轨道A、B给起重机轮子的反力。

解  (1)要使起重机不翻倒，应使作用在起重机上的所有力满足平衡条件。起重机所受的力如图2-26所示，即:载荷的重力W₁，机架的重力W₂，平衡块重W₀以及轨道的约束反力F_NA和F_NB。为使起重机不绕点B翻倒，在临界情况下，F_NA=0, 这时求出的W₀值是所允许的最小值。建立平衡方程式。

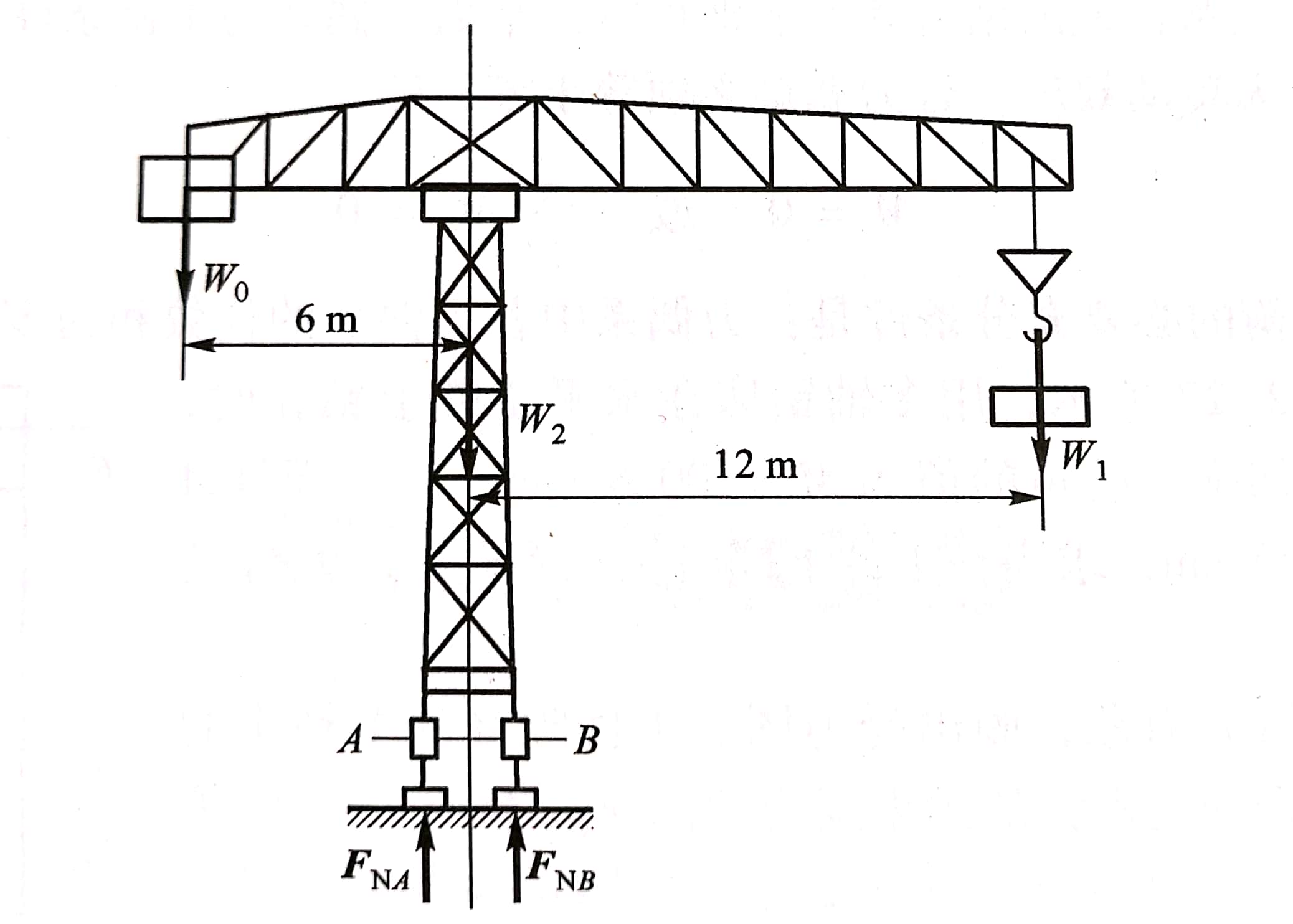
图2-26

当空载时，W₁=0，为使起重机不绕点A翻倒，在临界情况下，F_NB=0, 这时求出的W₀值是所允许的最大值。

起重机实际工作时不允许处于极限状态，要使起重机不会翻倒，平衡块的重量应在这两者之间，即

(2) 取W₀= 180kN， 求满载时作用于轮子的约束反力F_NA和F_NB。此时，起重机在W₀、W₁、W₂及F_NA、F_NB作用下平衡。于是有:

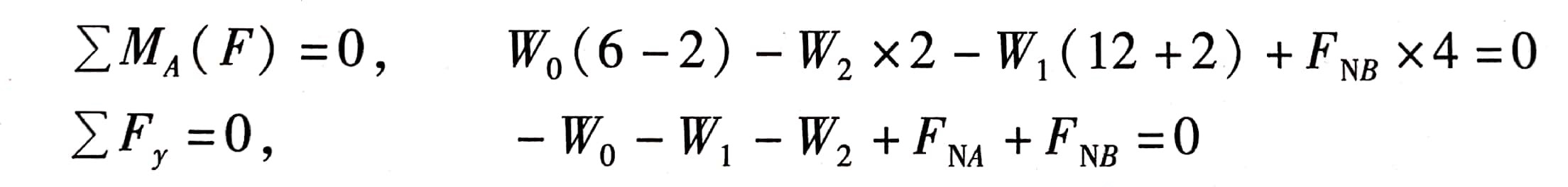
得

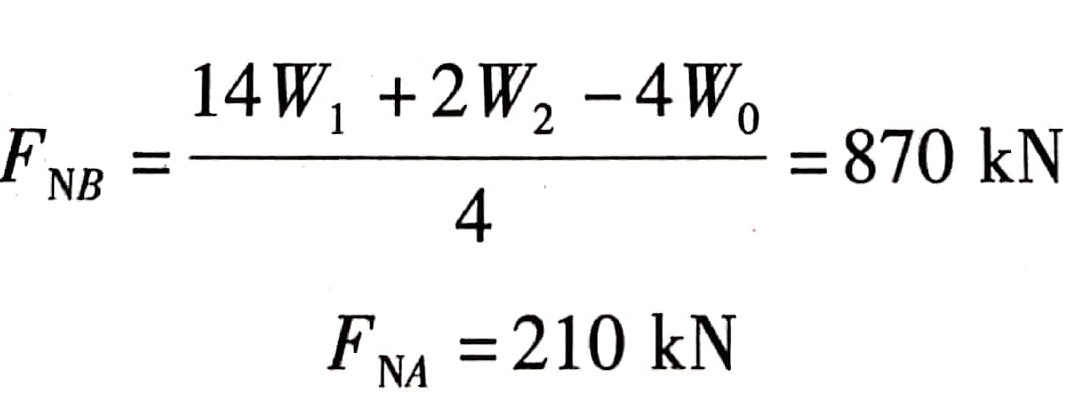
作用在物体同一平面内力的许多力偶， 称为平面力偶系。由于力偶矩是一个代数量，因此平面内力偶系的任意个力偶可以合成一个合力偶，合力偶矩( M)等于平面力偶系中各力偶矩的代数和，表示为

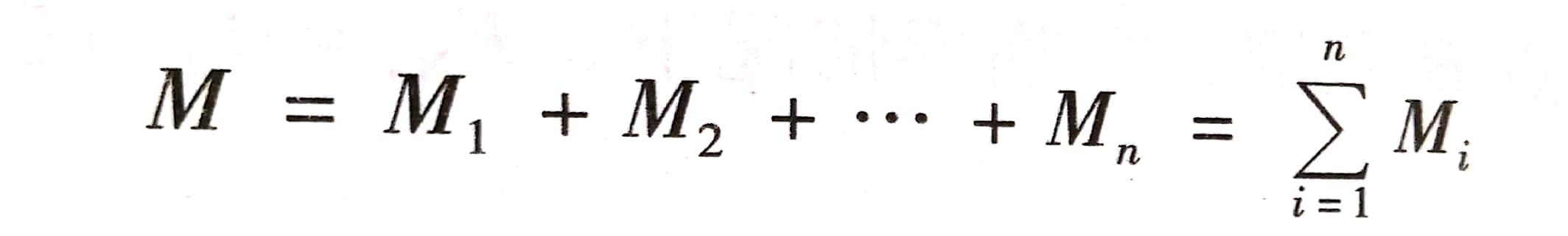     （2-9）

知道了平面力偶系合成的结果和方法即可推出平面力偶系的平衡条件。若使平面力偶系达到平衡，即力偶系无转动效应，合力偶矩必须等于零，即

    (2- 10)

平面力偶系平衡的必要充分条件是:力偶系中各力偶矩的代数和为零。

例2-8 如图2-27 所示，用多轴钻床在水平工件上钻孔时，每个钻头对工件的切削力偶矩的值为M=100N?m，固定螺柱A和B的距离l=1500 mm,求当在工件上同时钻三个孔时，两螺柱所受的水平力。

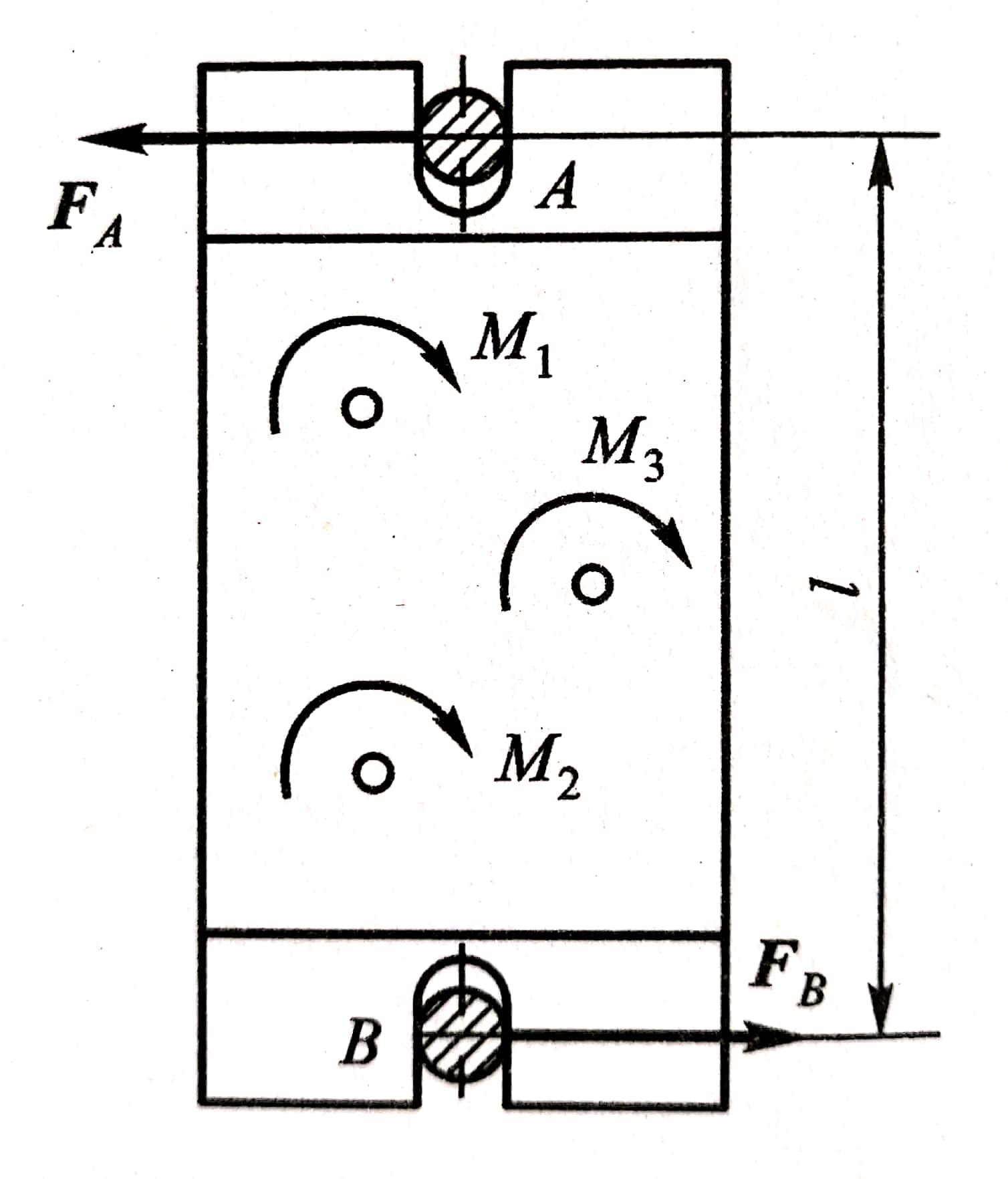
图2-27

解  选工件为研究对象，画出受力图。工件除受三个钻头的切削力外，还受两个固定螺柱的约束反力F_A、F_B。 由力偶系的平衡条件知:

得 

代入已知数值，F_A=200N, 因为F_A是正值，所以图设方向正确。

又因为

所以