加工路线的确定首先必须保持被加工零件的尺寸精度和表面质量，其次考虑数值计算简单、走刀路线尽量短、效率较高等问题。因精加工的进给路线基本上都是沿其零件轮廓顺序进行的，因此确定进给路线的工作重点是确定粗加工及空行程的进给路线。

在数控车床还未达到普及使用的情况下，一般应把毛坯件上过多的余量，特别是含有锻铸硬皮层的余量安排在普通车床上加工，当必须用数控车床加工时，则要注意程序的灵活安排，可安排一些子程序对余量过多的部位先做一定的切削加工。

(1)对大余量毛坯进行阶梯切削时的加工路线，如图1所示为车削大余量工件的两种加工路线，图1(a)是错误的阶梯切削路线，图1(b)按1→5的顺序切削，每次切削所留余量相等，是正确的阶梯切削路线。因为在同样背吃刀量的条件下，按图1(a)方式加工所剩的余量过多。

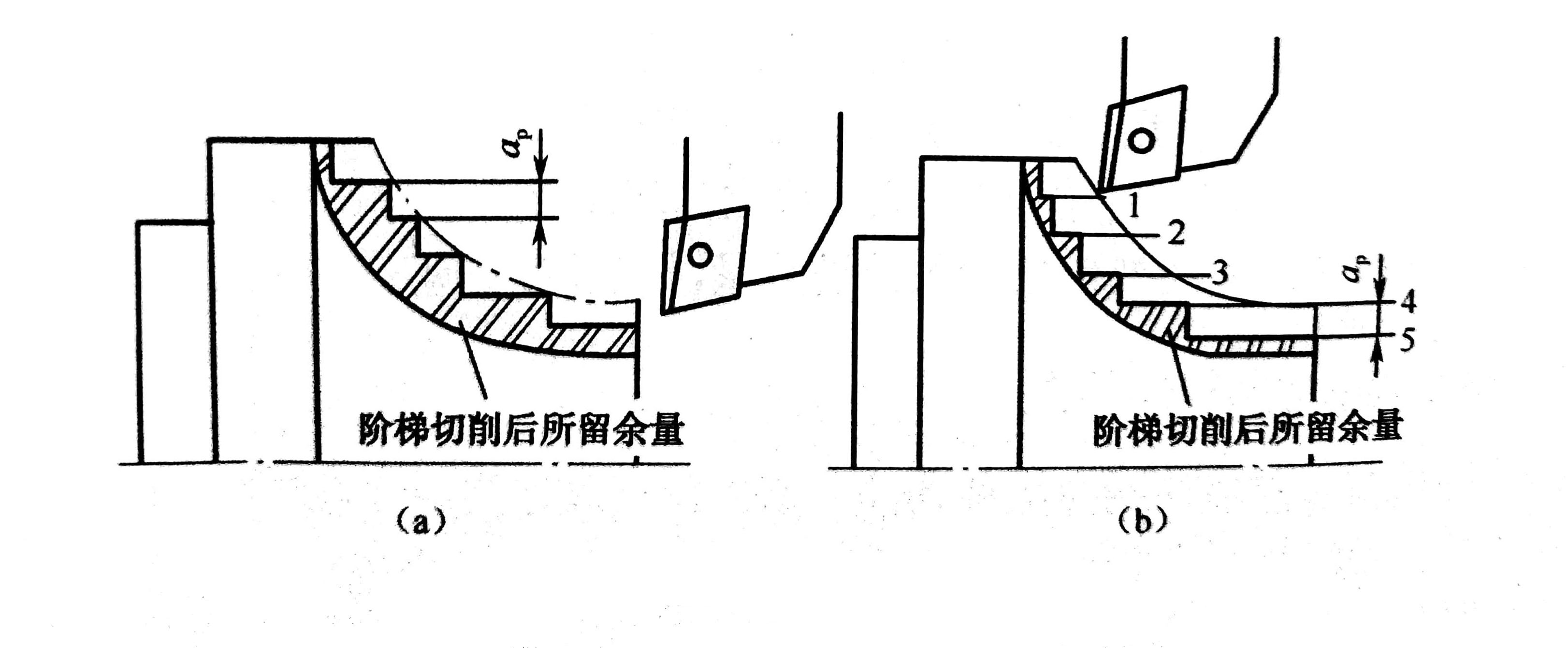
图1 车削大余量毛坯的阶梯路线

根据数控加工的特点，还可以放弃常用的阶梯车削法，改用依次从轴向和径向进刀、顺工件毛坯轮廓走刀的路线，如图2所示。

(2)分层切削时刀具的终止位置。当某表面的余量较多需分层多次走刀切削时，从第二刀开始就要注意防止走刀到终点时切削深度的猛增。如图3所示，设以90°主偏角刀分层车削外圆合理的安排应是每一刀的切削终点依次提前一小段距离e(如可取e=0.05mm)。如果e=0，则每刀都终止在同一轴向位置上，主切削刃就可能受到瞬时的重负荷冲击。当刀具的主偏角大于90°,但仍然接近90°时，也宜做出层层递退的安排，经验表明，这对延长粗加工刀具的寿命是有利的。

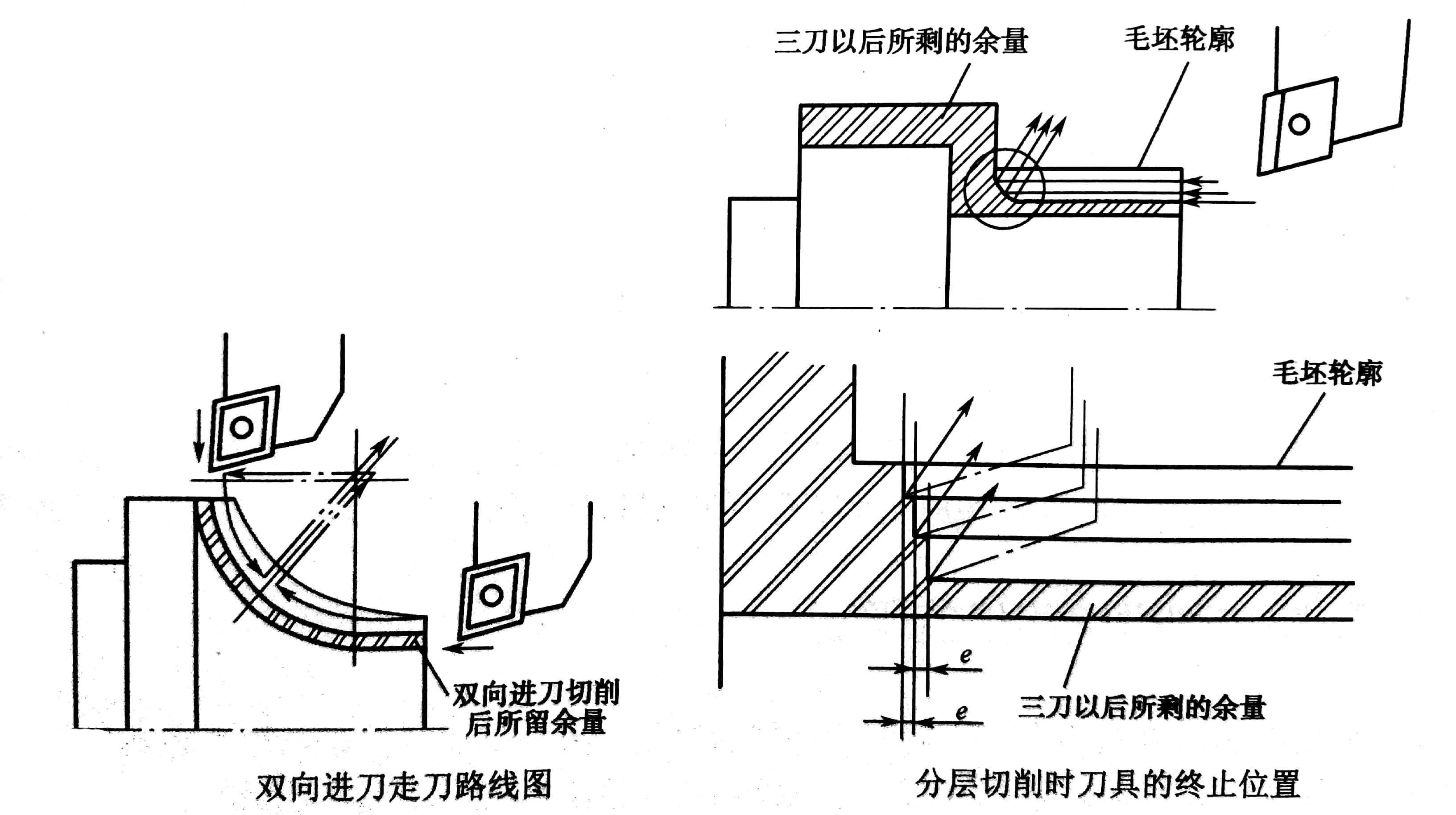
左图2 右图3

在数控机床上进行加工时，要安排好刀具的切入切出路线，尽量使刀具沿轮廓的切线方向切入/切出。尤其是车螺纹时，必须设置升速段δ₁和降速段δ₂，如图4所示，这样可避免因车刀升降而影响螺距的稳定。

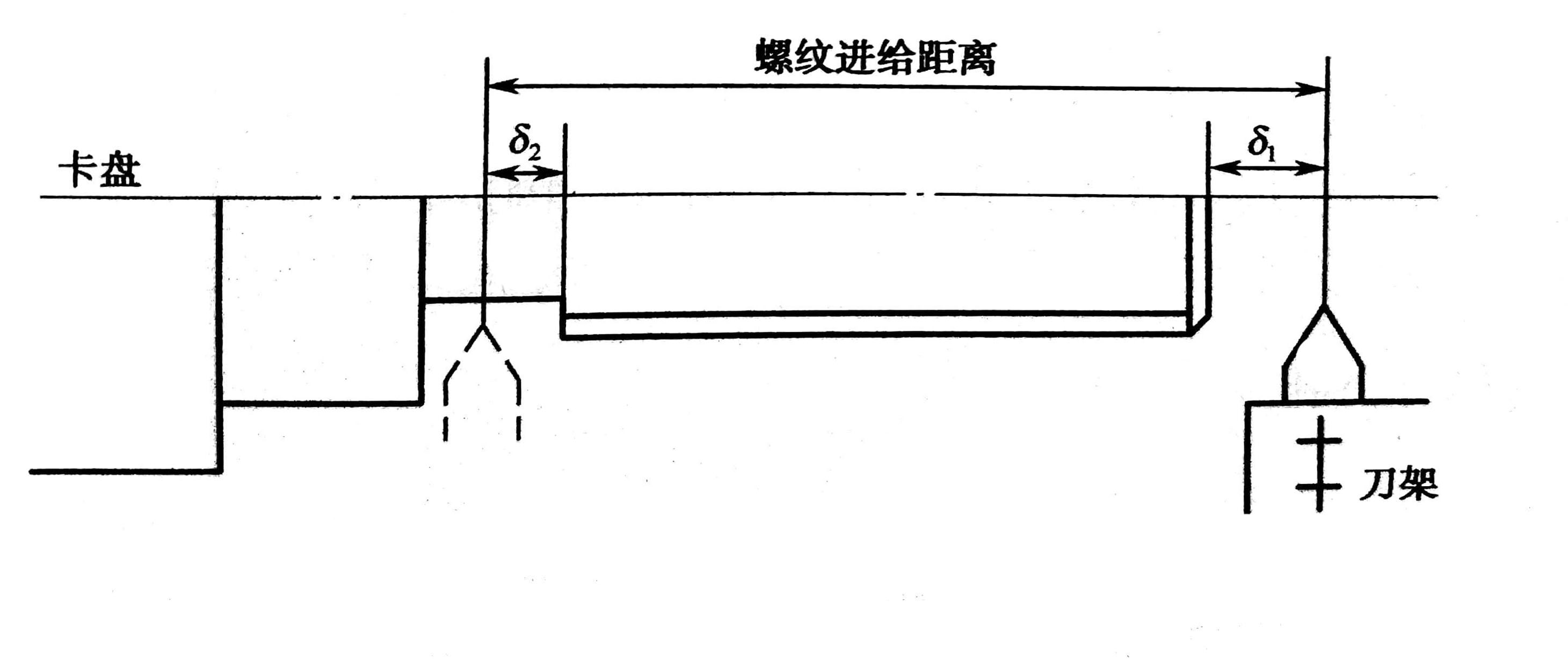
图4 车螺纹时的升速段和降速段

确定最短的走刀路线，除了依靠大量的实践经验外，还应善于分析，必要时辅以一些简单计算。现将实践中的部分设计方法或思路介绍如下：

(1)巧用对刀点。图5(a)为采用矩形循环方式进行粗车的一般情况示例。其起刀点A的设定是考虑到精车等加工过程中需方便地换刀，故设置在离坯料较远的位置处，同时将起刀点与其对刀点重合在一起，按三刀粗车的走刀路线安排如下：

第一刀为A→B→C→D→A

第二刀为A→E→F→G→A

第三刀为A→H→I→J→A

图5(b)则是将起刀点与对刀点分离，并设于B点位置，仍按相同的切削用量进行三刀粗车，起刀点与对刀点分离的空行程为A→B。

第一刀为B→C→D→E→B

第二刀为B→F→G→H→B

第三刀为B→I→J→K→B

显然，图5(b)所示的走刀路线短

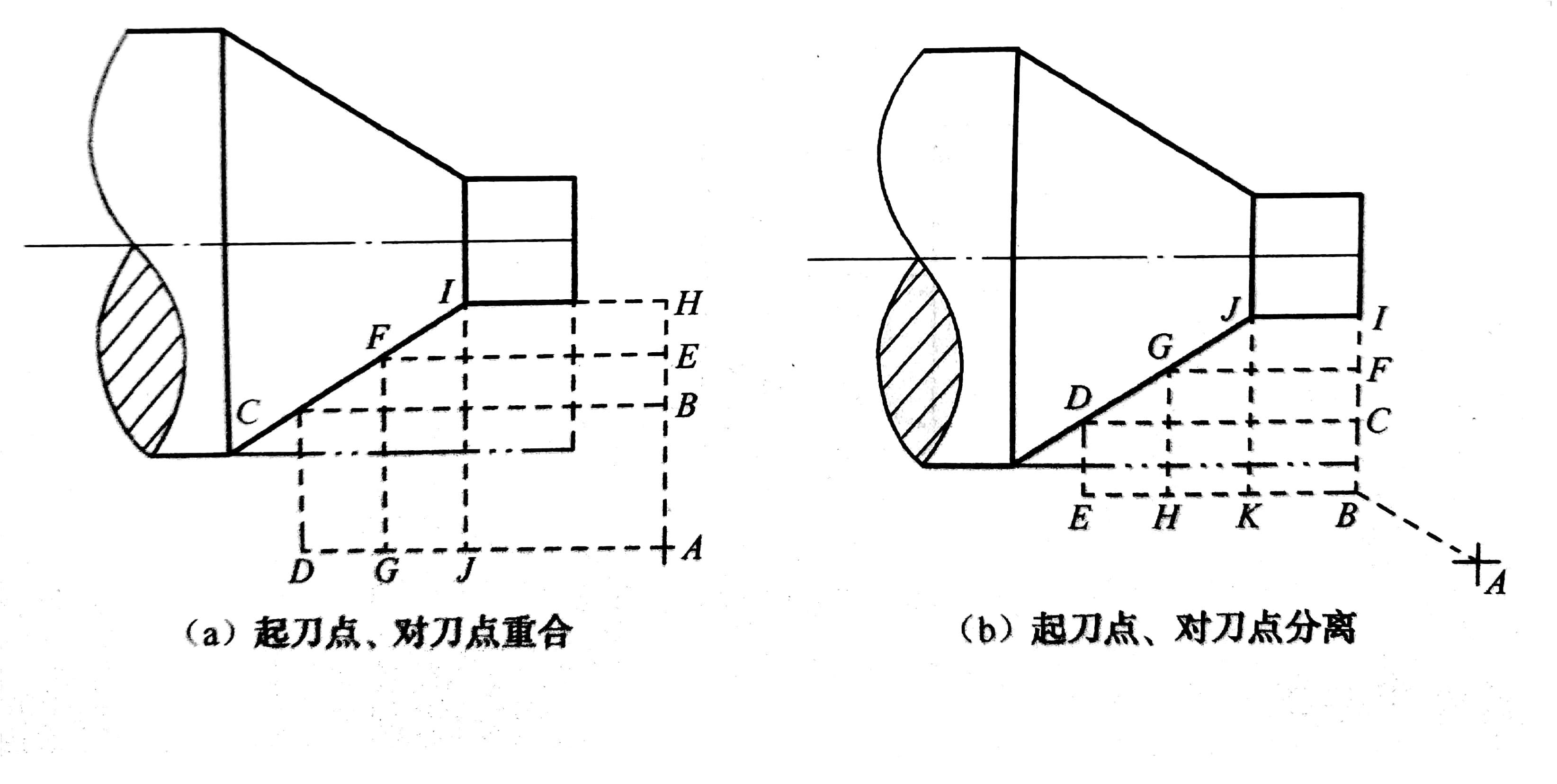
图5 巧用对刀点

(2)巧设换刀点，为了考虑换(转)刀的方使和安全，有时将换(转)刀点也设置在离件较远的位置处(如图5中的A点)，那么，当换第二把车刀后，进行精车时的空行程路线必然也较长；如果将第二把车刀的换刀点也设置在图5(b)中的B点位置上，则可缩短空行程距离。

(3)合理安排“回零”路线，在手工编制较复杂轮廓的加工程序时，为使其计算过程尽量简化，既不易出错，又便于校核，编程者(特别是初学者)有时将每一刀加工完后的刀具终点通过执行“回零”(即返回对刀点)指令，使其全都返回到对刀点位置，然后再进行后续程序。这样会增加走刀路线的距离，从而大大降低生产效率，因此，在合理安排“回零”路线时，应使其前一刀终点与后一刀起点间的距离尽量缩短，或者为零，即可满足走刀路线最短的要求。

切削进给路线短，可有效地提高生产效率，降低刀具损耗等，在安排粗加工或半精加工的切削进给路线时，应同时兼顾到被加工零件的刚性及加工的工艺性等要求，不要顾此失彼。

1)常用的粗车走刀路线

如图6所示为粗车工件时几种不同切削进给路线的安排示例，其中，图6(a)表示利用数控系统具有的封闭式复合循环功能而控制车刀沿着工件轮廓进行走刀的路线：图6(b)为利用其程序循环功能安排的“三角形”走刀路线：图6(c)为利用其矩形循环功能而安排的“矩形”走刀路线。

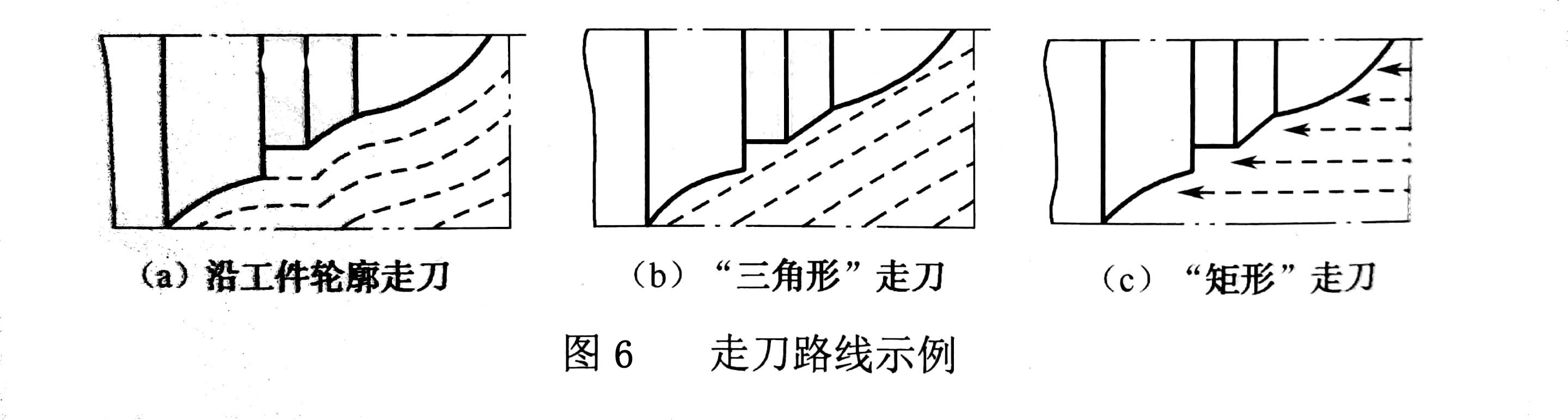
2)车圆锥走刀路线

车圆锥有三种加工路线，如图7所示。图7(a)需要计算终刀距S(由相似三角形可算出)，这种走刀路线较短图7(b)不需要计算S，只要确定背吃刀量a_p即可，此种方式编程方便，但在每次切削中背吃刀量是变化的，而且刀具切削路线较长，图7(c)走阶梯路线，假设先粗车两刀，最后精车一刀，两刀粗车的终刀距S要做精确计算，此种加工路线粗车时背吃刀量相同，而精车时背吃刀量不同，不过刀具的切削运动路线最短。

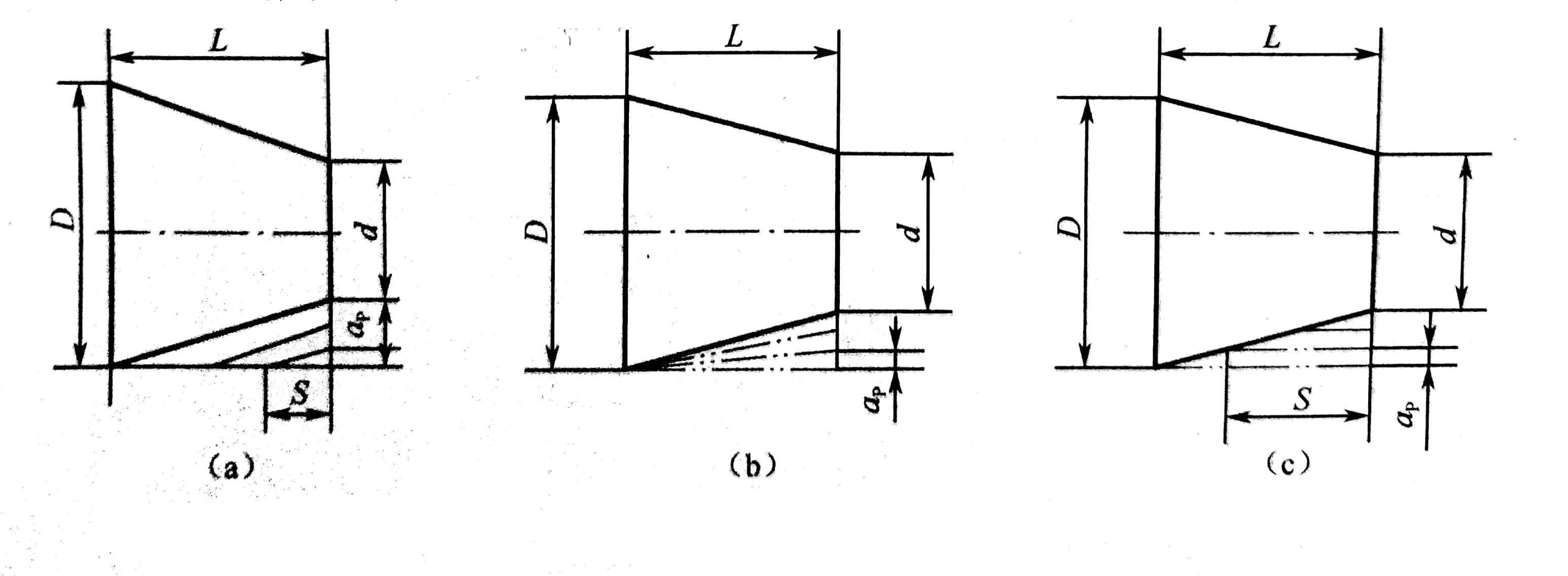
图7 车圆弧的走刀路径

3)车圆弧走刀路线

在粗加工圆弧时，因其切削余量大而且不均匀，若一刀把圆弧切出来，很容易打刀，必须多刀切削，先将大部分余量去除，最后车得圆弧轮廓。图8所示为车圆弧常用的走刀路线，图8(a)为车圆法，即用不同半径的圆来多刀车削圆弧。该方法在确定了每次背吃刀量a_p后，对90°圆弧的起点、终点比较容易确定，编程方便，常用来加工复杂圆弧，但加工凸圆弧时空行程较长。图8(b)为车矩形法，即先粗车成阶梯，最后一刀精车圆弧，该方法在确定了背吃刀量a_p后，需要精确计算出粗车的终刀距S。该法刀具走刀路线较短，但数值计算烦琐。图8(c)为车锥法，即先车一个圆锥，再车圆弧。要注意车锥时的起点和终点的确定必须合理，否则可能会损坏圆弧表面，也可能将余量留得过大。该法计算较烦琐，但刀具切削路线最短。

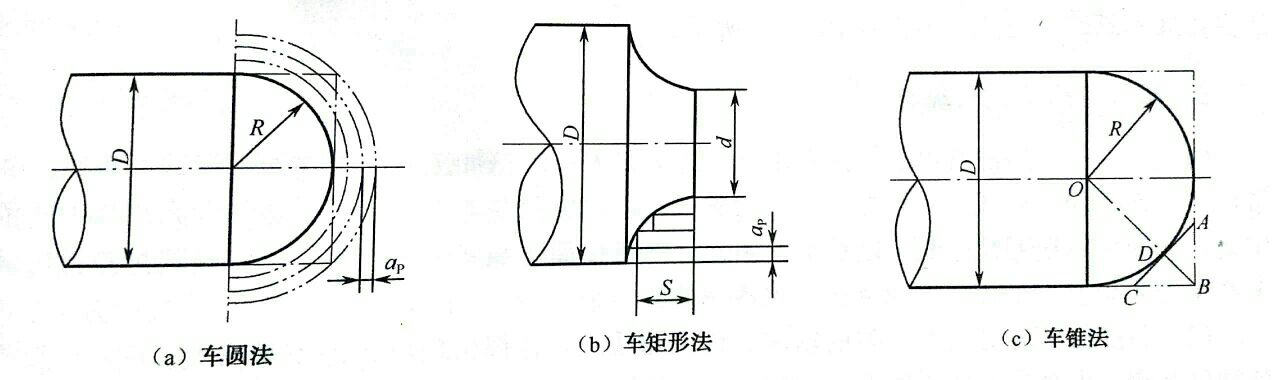
图8 车圆弧的走刀路线

4)车槽走刀路线

(1)对于宽度较窄、深度不大且精度要求不高的槽，可采用与槽等宽的刀具，采用直进法次进给成型加工，如图9(a)所示。刀具切入到槽底后可利用进给暂停指令使刀具短暂停留，以修整槽底圆度，提升槽壁的表面质量，退出过程中可采用工进速度。

(2)对于宽槽的切削，一般宽度、深度的精度及表面质量要求相对较高，在切宽槽时采用排刀的方式，选择小于槽宽的切槽刀进行粗切，在槽的两侧和槽底留有精加工余量，再用精切槽刀沿槽的一侧切至槽底，精加工槽底至槽的另一侧，再沿侧面退出，如图9(b)所示。

(3)车较小的圆弧槽时，一般用成型刀车削，如图9(c)所示。

(4)车较小的梯形槽时，一般用成型刀直进车削完成：车较大的梯形槽时，通常先车直槽再用梯形刀直进法或者左右切削法完成，如图9(d)所示。

5)对于深槽，宽度值不大但较深，为避免切槽过程中由于排屑不畅，出现扎刀或折断刀具的现象，应采用分次进刀的方式。刀具在切入工件一定深度后，停止进刀并退回一段距离，达到排屑和断屑的目的，如图9(c)所示。

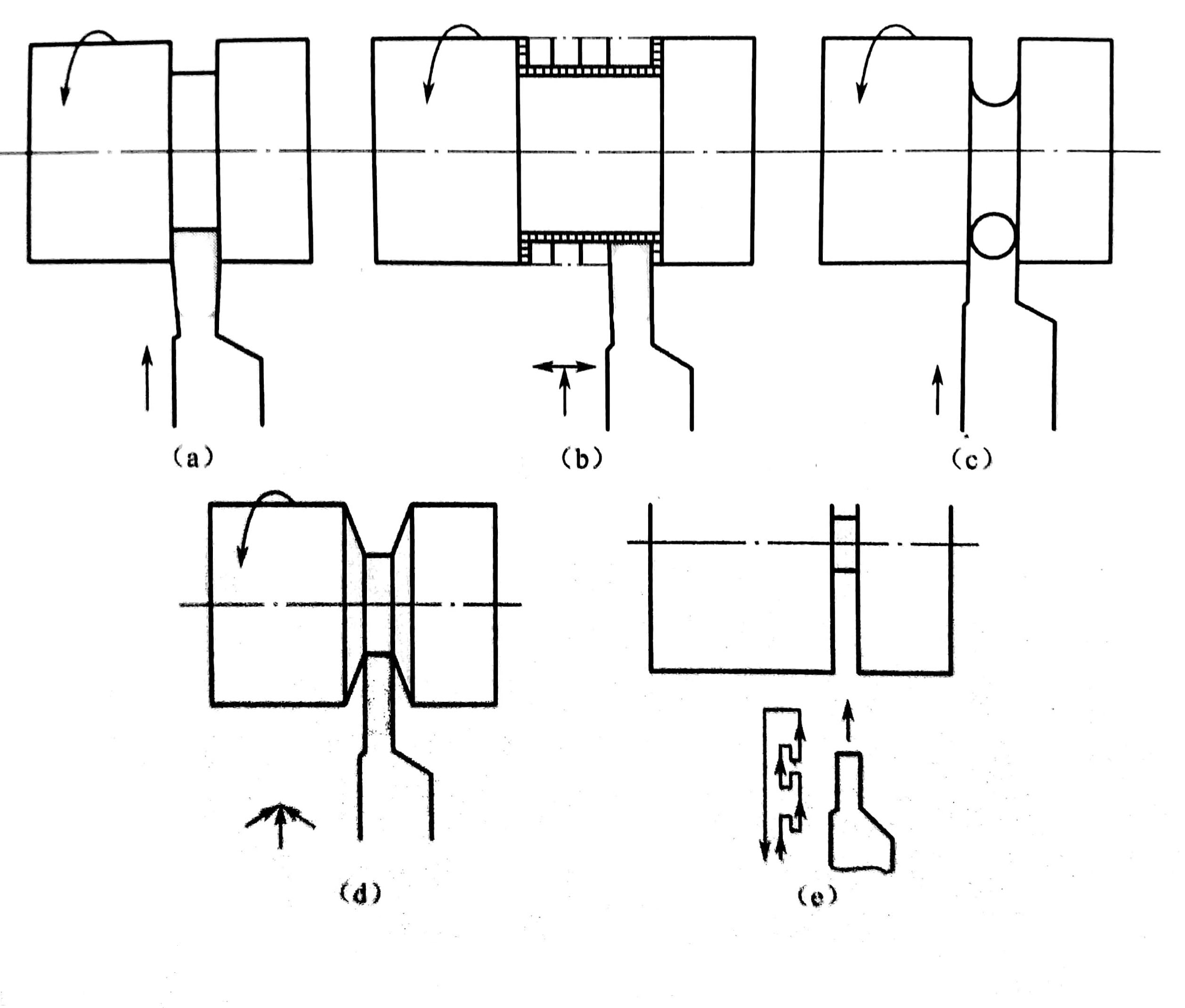
图9 车槽的进给路线

(1)最终轮廓的进给路线，在安排一刀或多刀进行的精加工进给路线时，其最终轮廓应由最后一刀连续加工而成，并且加工刀具的进刀、退刀位置要考虑妥当，尽量不要在连续的轮廓中切入和切出或换刀及停顿，以免因切削力突然变化而造成零件弹性变形，致使光滑连接轮廓上产生表面划伤、形状突变或滞留刀痕等缺陷。

(2)各部位精度要求不一致的精加工进给路线。若各部位精度相差不是很大，则应以最严的精度为准，连续走刀加工所有部位：若各部位精度相差很大，则精度接近的表面安排在同把刀走刀路线内加工，并先加工精度较低的部位，最后再单独安排精度高的部位的走刀路线。