如图所示，两直线的相对位置有三种:平行，相交，交叉(既不平行，又不相交，即不在同一平面上，称这两直线不共面亦称异面)。

如图a所示，过平行两直线AB CD上各点的投射线所形成的两个平面互相平行，它们与V面的交线也互相平行，即a'b'//c'd’。同理可证:ab//cd;a''b"//c"d''。

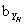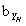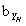如图b所示,AB与BC交于B.则B是两直线的共有点,b'应同时位于a'b'和b'c'上，即在这两条直线的V面投影的交点处。同理可证:b和b”也应分别位于这两条直线的同面投影的交点处。由于b、b'、b"是点B的三面投影,因而可知它们应符合一点的三面投影特性:b'b⊥OX、b'b"⊥OZ、b⊥OY_H、b"⊥OY_W和O=O或O、O,延长后交会于过原点O的45°铺助线上的同一点。

如图c所示，虽然a'b'与c'd'相交，而它们的交点是分别位于AB、CD上的对V面投影的重影点E、F的投影e'(f'),因而AB和CD不共面,是交叉两直线。由于E在F之前，所以e是可见点E的投影,(f')是不可见点F的投影。

由于交叉两直线在空间既不相交，又不平行，所以若它们的三对同面投影都相交，则如表中所示,同面投影的交点不能符合一点的三面投影特性:此外，也可能它们的同面投影有一对或两对相交,其余的同面投影分别平行。上述两种情况都表明了交叉两直线的投影既不符合平行两直线的投影特性，也不符合相交两直线的投影特性。

由前面的讨论可归纳出:两直线的相对位置在投影图中具有表所示的投影特性。

两直线的相对位置的投影特性

情况	平行两直线	相交两直线	交叉两直线
投 影 图
投 影 特 性	三对同面投影都分别互相平行	三对同面投影都分别相交，且投影的交点符合点的三面投影特性。	既不符合平行两直线的投影特性，又不符合相交两直线的视影特性。